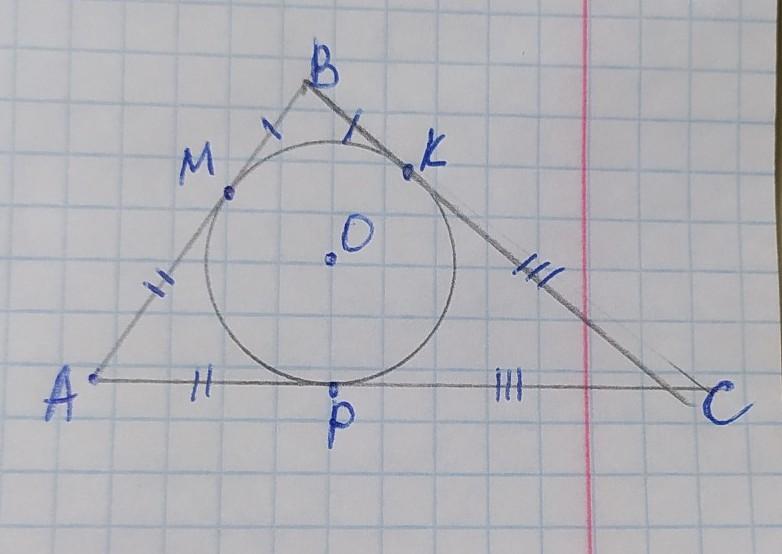
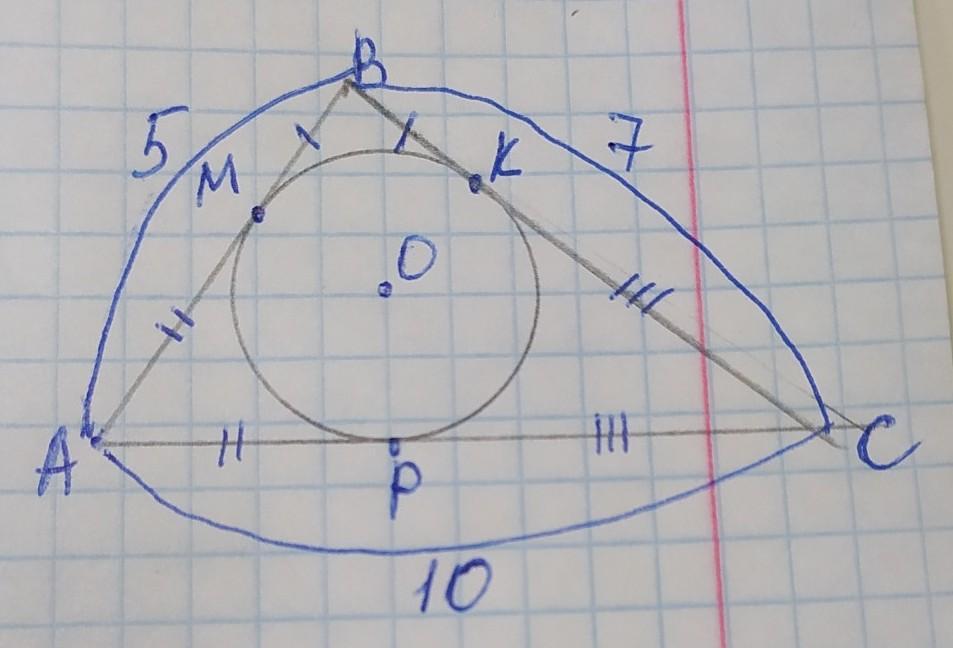
В треугольник со сторонами 5, 7 и 10 вписана окружность. Определите длины отрезков, на которые вписанная окружность разбила стороны треугольника.
В ответе должно быть 6 чисел.

Ответ:

ВМ=1

ВК=1

АМ=4

АР=4

КС=6

РС=6

Объяснение:

обозначим вершины треугольника А В С, точки касания М, К, Р, а центр вписанной окружности О. Стороны треугольника являются касательными к вписанной окружности, и отрезки касательных соединяясь в одной вершине равны от вершины до точки касания, поэтому: ВМ=ВК, АМ=АР, КС=РС. Пусть ВМ=ВК=х, тогда АМ=РМ=5–х, КС=РС=7–х. В этом случае сторона АС=АР+РС. Составим уравнение:

(5–х)+(7–х)=10

5–х+7–х=10

–2х+12=10

–2х=10–12

–2х= –2

х= –2÷(–2)

х=1

Итак: ВМ=ВК=1, тогда АМ=АР=5–1=4

КС=РС=7–1=6