Предмет: Геометрия, автор: asaprockikill3

Образующая конуса наклонена к плоскости основания под углом 30°. Найдите длину образующей, если объём конуса равен 216п (п - пи, которое 3,14....)

Ответы

Автор ответа: Miroslava227

Ответ:

$V = \frac{1}{3} \pi {r}^{2} h \\$

выразим высоту через радиус:

$tg30^{\circ} = \frac{h}{r} \\ h = \frac{ \sqrt{3} }{3} r$

подставим высоту в формулу объёма и найдем радиус

$\frac{1}{3} \times \pi {r}^{2} \times \frac{ \sqrt{3} }{3} r = 216\pi \\ {r}^{3} = 216 \times \frac{9}{ \sqrt{3} } \\ {r}^{3} = 261 \times 3\sqrt{3} \\ r = \sqrt[3]{216 \times 3 \sqrt{3} } = \\ = \sqrt[3]{ {6}^{3} \times {( \sqrt{3}) }^{3} } = 6 \sqrt{3}$

Найдем образующую:

$\cos(30^{\circ}) = \frac{r}{l} \\ l = \frac{r}{ \cos(30^{\circ}) } = 6 \sqrt{3} \times \frac{2}{ \sqrt{3} } = 12$

Ответ: 12 см

Приложения:

Предыдущий вопрос

Следующий вопрос

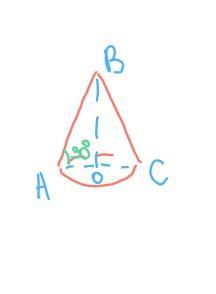
Интересные вопросы

Предмет: Окружающий мир, автор: vika314

как узнать сколько воды в теле9 летнего ребенка

2 года назад

Предмет: Русский язык, автор: неззнайка

наливные яблоки на ветке падеж?

2 года назад

Предмет: Английский язык, автор: elalexeevna201

Закончите предложения,употребляя сложное дополнение
1.Complete the sentences, using complex object.

Model: “Bring me a book, “ said my brother to me. →My brother wanted me to bring him a book.
6. ‘Wait for me after school,’ said Ann to me. – Ann wanted …………… 7. ‘Fix the shelf in the kitchen,’ my father said to me. – My father expected …………… 8. ‘It will be very good if you study English,’ said my mother to me. – My mother wanted …………..… 9. ‘Bring me some water from the river, children,’ said our grandmother. – Our grandmother wanted ……………… 10. ‘Come to my birthday party,’ said Kate to her classmates. – Kate expected …………….… 11. The biology teacher said to us: ‘Collect some insects in summer.. – The biology teacher would like …………..… 12. ‘Don’t eat ice cream before dinner’ said our mother to us. Ourmotherdidnotwant