с самолёта летящего горизонтально и прямолинейно на высоте определены углы А=45* и В=30*, обозначающие начало и конец взлетной полосы длиной 1000м. Определить угол С, и высоту АС, на которой летит самолёт .
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО 100 баллов !!!!!!!

Ответ:

∠C = 105°

AC = 515,5 м

CK = 364,5 м

Примечание:

Объяснение:

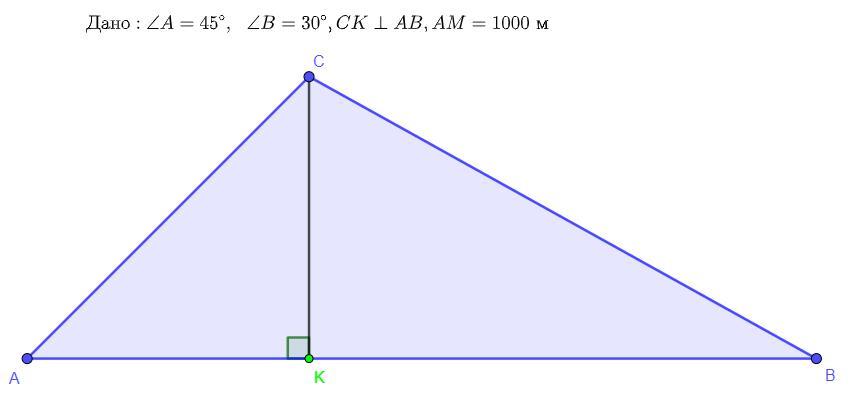
Дано: ∠A = 45°, ∠B = 30°, AB = 1000 м, AB = 1000 м, CK ⊥ AB

Найти: ∠C, AC, CK - ?

Решение:

По теореме про сумму углов треугольника (треугольник ΔABC):

∠A + ∠B + ∠C = 180° ⇒ ∠C = 180° - ∠A - ∠B = 180° - 45° - 30° = 105°.

По теореме синусов:

.

Рассмотрим прямоугольный треугольник ΔCAK(по условию CK ⊥ AB)

По определению синуса в прямоугольном треугольнике:

м.