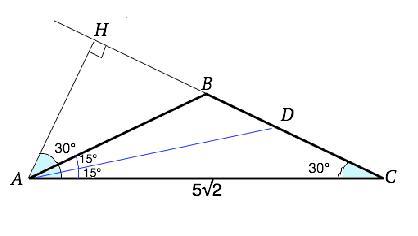
В равнобедренном треугольнике ABC, основание AC= 5 корень из 2, угол А = 30 градусов. Найдите длину его биссектрисы AD

Ответ: AD=5

Объяснение:

      ∆ АВС - равнобедренный, ⇒ ∠В=180°-2•30°=120°

Продлим СВ и проведем из вершины А перпендикуляр АН. Угол НВА - смежный углу АВС и равен 60°, угол НАВ=30°

     ∆ АСН - прямоугольный, катет АН противолежит углу 30° и равен половине гипотенузы АС.

АН=АС:2=(5√2):2

    Так как АD - биссектриса, ∠ВАD=30°:2=15°, ⇒  

∠НАD=30°+15°=45°

∆ АНD - прямоугольный, ⇒

Из суммы углов треугольника ∠НDA=∠HAD=45°,

DH=AH=(5√2):2

AD=AH/sin45°=[5√2):2]:√2/2

AD=5