Предмет: Геометрия, автор: ritinabadasian45695

Помогите пожалуйста решить

Приложения:

Ответы

Автор ответа: NNNLLL54

Ответ:

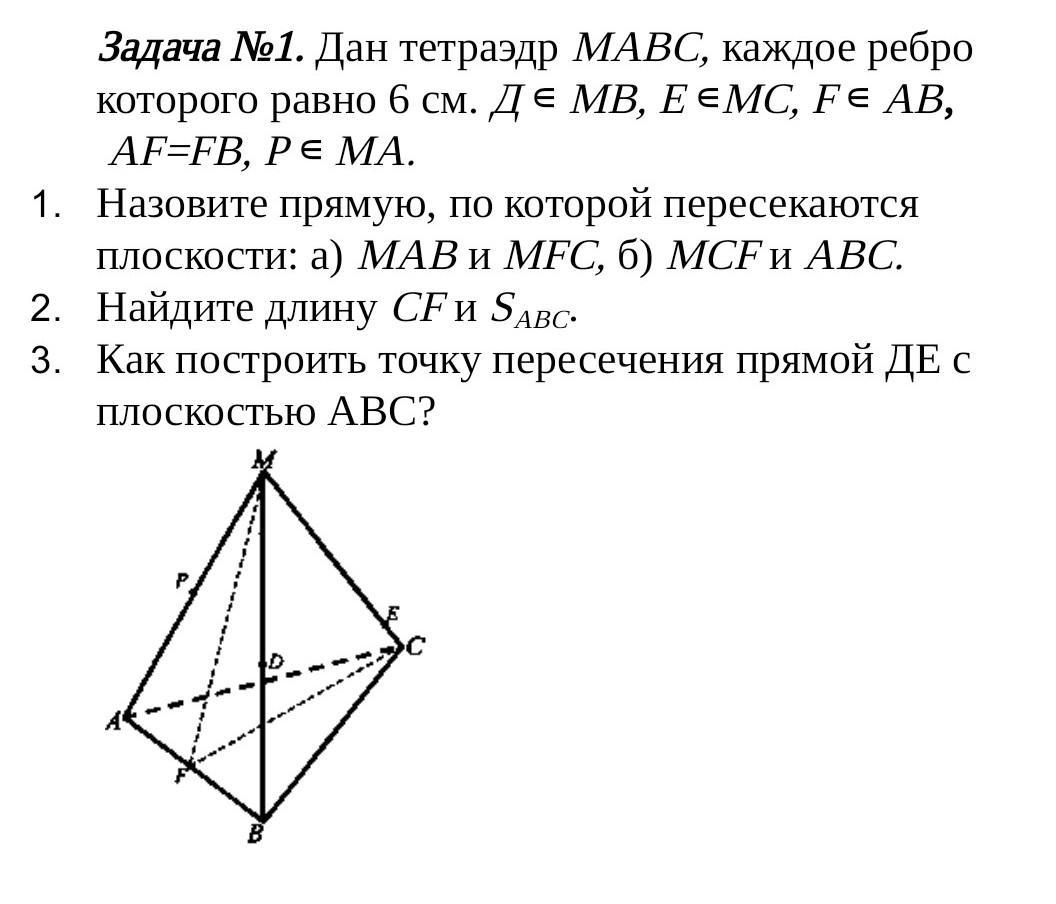
МАВС - тетраэдр , все рёбра = 6 см ⇒ ΔАВС - равносторонний треугольник со стороной в 6 см .

1a) плоскость МАВ ∩ пл. MFC = MF ,

1б) пл. MCF ∩ пл. ABC = CF

2) СF - высота, биссектриса и медиана равностороннего ΔАВС , поэтому она равна

$CF=\sqrt{BC^2-BF^2}=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{27}=3\sqrt3$ см

Так как ΔАВС равносторонний, то все его углы равны 60° ⇒

$S(ABC)=\dfrac{1}{2}\cdot AB\cdot AC\cdot sin60^\circ =\dfrac{1}{2}\cdot 6\cdot 6\cdot \dfrac{\sqrt3}{2}=9\sqrt3$ см²

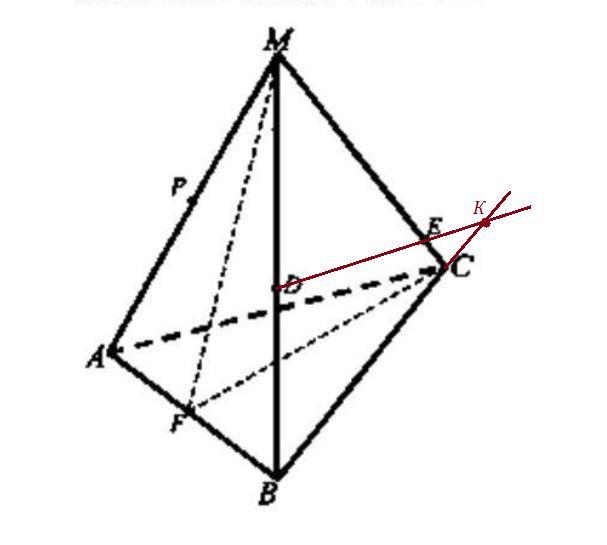
3) Чтобы построить точку пересечения прямой DE и плоскости АВС , надо продлить сторону ВС до пересечения с прямой DE . Получим точку К . Смотри рисунок .

Приложения: