Предмет: Математика,
автор: kasindana892
доказать что следующие неравенства не имеют решений
Приложения:
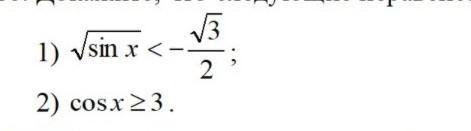
Ответы
Автор ответа:
0
Ответ:
1. Квадратный корень по определению положительное число, значит левая часть не может быть меньше отрицательного числа.
2. косинус меняется от -1 до 1, значит не может быть больше либо равен 3.
Автор ответа:
0
• Давай начнём со второго (он проще):
cos(x) ≥ 3
• Область значений косинуса (E (y)):
-1 ≤ cos(x) ≤ 1 {=} |cos(x)| ≤ 1
Т.е. простыми словами, косинус принимает только эти значения)
Но 3 > 1, ⇒ cos(x) не может быть больше или равен 3,
⇒ cos(x) ≥ 3 - не имеет решений
• Теперь разберёмся с первым
√sin(x) < -√3/2
• Очевидно, что корень из любого действительного числа не может быть меньше отрицательного числа, потому что:
√а ≥ 0
• Отсюда и делаем вывод, что:
√sin(x) < - √3/2 - не имеет решений
Можно лучший ответ?
Интересные вопросы
Предмет: Другие предметы,
автор: Огурченко
Предмет: Қазақ тiлi,
автор: арука2975
Предмет: Русский язык,
автор: Mashutlaps
Предмет: Русский язык,
автор: котик1055
Предмет: Немецкий язык,
автор: Аноним