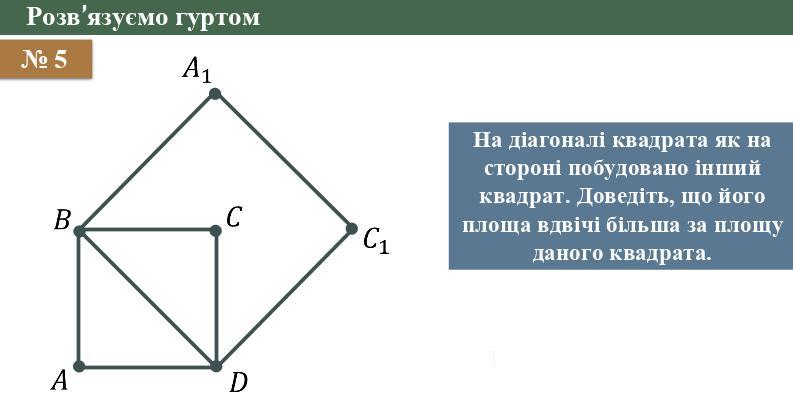
На дiагоналi квадрата як на сторонi побудовано iнший квадрат. Доведiть, що його площа вдвiчi бiльша за площу даного квадрата

Ответ:

Площадь квадрата А1ВDC2 больше в 2 раза площади квадрата ABCD.

Объяснение:

Пусть сторона АВ будет а.

АВ=а

Диагональ квадрата будет

ВD=a√2 (диагональ квадрата и сторона большего квадрата)

Площадь квадрата ABCD

S(ABCD)=AB²=a²

Площадь квадрата А1ВDC1

S(A1BDC1)=BD²=(a√2)²=a²*2=2a²

2a²/a=2 раза площадь квадрата (А1ВDC1) больше площади квадрата (ABCD)