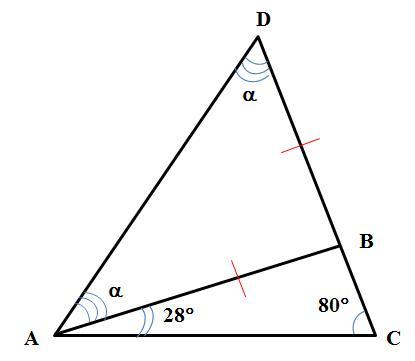
Сторона BC треугольника ABC продолжена за точку B. На продолжении отмечена точка D так,что AB=BD. Найдите величину угла BAD,если угол ACВ равен 80*,а угол BAC равен 28*. Ответ дайте в градусах. Запишите решение и ответ.

Ответ:

∠BAD=36°

Объяснение:

Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом.

В силу этой теоремы сумма углов BAD и BDA треугольника ABD равна внешнему углу при вершине B (см. рисунок), то есть углу ABC треугольника ABC: ∠ABC=∠BAD+∠BDA.

По теореме о внутренних углах треугольника

∠ABC+∠ACB+∠BAC=180° или ∠ABC=180°-∠ACB-∠BAC=180°-80°-28°=72°.

Так как в треугольнике ABD для сторон имеет место равенство AB=BD, то треугольник ABD равнобедренный. В равнобедренном треугольнике углы при основании равны, то есть α=∠BAD=∠BDA. Тогда ∠ABC=2·∠BAD или ∠BAD=∠ABC:2=72°:2=36°.