Предмет: Алгебра, автор: okssuhowa

Помогите вычислить (фото)

Приложения:

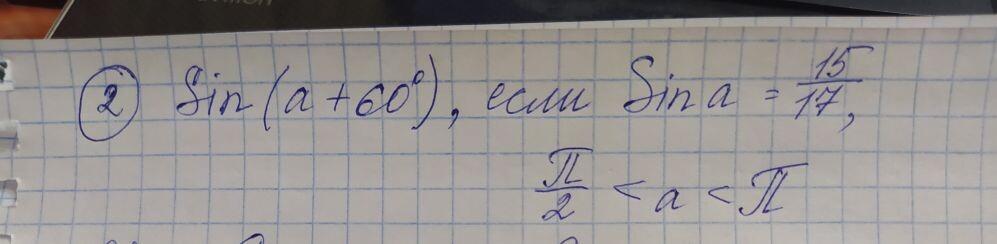
Ответы

Автор ответа: Miroslava227

Ответ:

$\sin( \alpha + 60^{\circ}) = \\ = \sin( \alpha ) \cos(60^{\circ}) + \cos( \alpha ) \sin(60^{\circ}) = \\ = \frac{1}{2} \sin( \alpha ) + \frac{ \sqrt{3} }{2} \cos( \alpha )$

угол принадлежит 2 четверти, косинус отрицательный

$\cos( \alpha ) = \sqrt{1 - \sin {}^{2} ( \alpha ) } \\ \cos( \alpha ) = - \sqrt{1 - \frac{225}{289} } = - \sqrt{ \frac{64}{289} } = - \frac{8}{17}$

$\sin( \alpha + 60) = \frac{1}{2} \times \frac{15}{17} + \frac{ \sqrt{3} }{2} \times ( - \frac{8}{17} ) = \\ = \frac{15 - 8 \sqrt{3} }{34}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: run2180913180

9 класс сочинение на ОГЭ Сочинение-рассуждение на тему "Что такое отзывчивость"

2 года назад

Предмет: Английский язык, автор: bossroma1971

как написать на англиском языке мой любимый из мультика персонаж и перевод

2 года назад

Предмет: Русский язык, автор: artem88001

ИЗ БУКВ КАЖДОГО СЛОВА СОСТАВЬТЕ НОВОЕ ЗАПИШИТЕ ПОЛУЧЕНОЕ СЛОВО ОПРЕДЕЛИТЕ РОД ПОДЧЕРКНИТЕ ПАРЫ СЛОВ КОТОРЫЕ ИМЕЮТ ИМЕЬТ ОДИН И ТОТ ЖЕ РОД ВЕСНА - НАВЕС : ЛЕТО- ...... СОСНА- ..... КОМАР-..... ЛОЖА-.... КУЛАК-.... КАМЫШ- .... УКЛОН- ...

2 года назад

Предмет: Математика, автор: aroora

Дачник придбав ділянку землі квадратної форми з периметром 200м за ціною 0.58 тис.грн за сотку.Він вирішив поставити огорожу з двома хвіртками шириною 1.25м кожна.Вартість однієї хвіртки дорівнює 0.36 тис.грн , а 45м огорожі коштують 1.8 тис.грн. Бригада робітників поставила огорожу за 2 дні, працюючи по 8 годин на день. Їх робота протягом однієї години коштує 0.1 тис.грн. Яка вартість ділянки землі? Яка вартість огорожі разом з її встановленням?

8 лет назад

Предмет: Литература, автор: DoctorMrak

уроки французского анализ эпизода когда учительница с мальчиком играли в чику

8 лет назад