Предмет: Алгебра, автор: HavaBekova2005ing

докажите тождество:
$\tan( \gamma ) + \cot( \gamma ) + \tan(3 \gamma ) + \cot(3 \gamma ) = \frac{8 \cos(2 \gamma ) ^{2} }{ \sin(6 \gamma ) }$

Приложения:

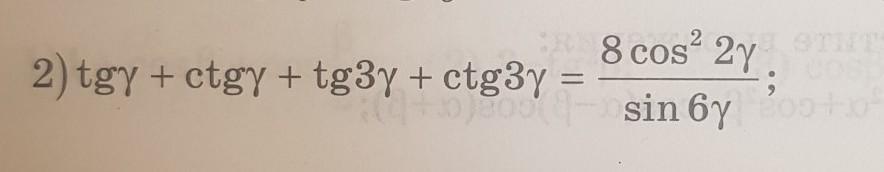
Ответы

Автор ответа: Universalka

1

$tg\alpha+Ctg\alpha +tg3\alpha+Ctg3\alpha=(tg\alpha+tg3\alpha) +(Ctg\alpha+Ctg3\alpha)=\\\\=\frac{Sin(\alpha+3\alpha)}{Cos\alpha Cos3\alpha} +\frac{Sin(\alpha+3\alpha)}{Sin\alpha Sin3\alpha} =\frac{Sin4\alpha}{Cos\alpha Cos3\alpha} +\frac{Sin4\alpha}{Sin\alpha Sin3\alpha}=\\\\=\frac{Sin4\alpha(Sin\alpha Sin3\alpha+Cos\alpha Cos3\alpha)}{Sin\alpha Cos\alpha Sin3\alpha Cos3\alpha} =\frac{Sin4\alpha*Cos(3\alpha-\alpha)}{\frac{1}{4}*2Sin\alpha Cos\alpha*2Sin3\alpha Cos3\alpha}=$

$=\frac{4Sin4\alpha Cos2\alpha}{Sin2\alpha Sin6\alpha} =\frac{4*2Sin2\alpha Cos2\alpha Cos2\alpha}{Sin2\alpha Sin6\alpha}=\boxed{\frac{8Cos^{2}2\alpha}{Sin6\alpha}}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: ропо2

С пишите , найдите в данных предложениях подлежащие и сказуемые . Определите, чем они выражены . Поставьте где необходимо тире . 1 Я последний поэт деревни . 2 Большое это удовольствие жить на земле . 3 Мои друзья загадка для меня . 4 Сердце не камень . 5 Лишнее говорить только делу вредить . Пожалуйста помогите

2 года назад

Предмет: Английский язык, автор: bublik909

Помогите пожалуйста с тестом :)1.You ... take care of your parents.
1.ought to
2.need to
3.are to
4.should to

2.The letter ... sent tomorrow.
1.will be
2.am
3.has
4.does

3.He’s doing … exercise now.
1.a
2.an
3.many
4.few

4.We thought they ... be late.
1.have
2.will
3.would
4.shall

5.They are busy with … lessons.
1.him
2.its
3.she
4.their

6.We ... to stay at home because it was raining.
1.will
2.has
3.had
4.have been

7.It is late. I ... go home.
1.need
2.must
3.can
4.may

8.My cat caught twenty … last year!

1.mice
2.mouses
3.mices
4.mouse

9.The student ... as an apprentice to a trained worker next week.

1.shall work
2.would work
3.woks
4.will work

10.When ... you finish writing your report?
1.are
2.is
3.have
4.did

2 года назад

Предмет: Русский язык, автор: вероника186

подчеркнуть слова,в корне которых есть безударный гласный звук.устно доказать правильность написания,море,дождинка,горка,письма,шестой,весна,трава,грибок,скворец,волна,слезы,садик,дома,грачи,записать,вода.

2 года назад

Предмет: Химия, автор: Savlad

Помогите! Я не знаю как найти ню.И все остальное.Помогите и обясните.

8 лет назад

Предмет: Русский язык, автор: Настюша123Сулаеман

Установите соответствие
Быстроходный
Сталелитейный
Высококачественный
Вид связи:
1)Согласование
2)Примыкание
3)Управление

8 лет назад