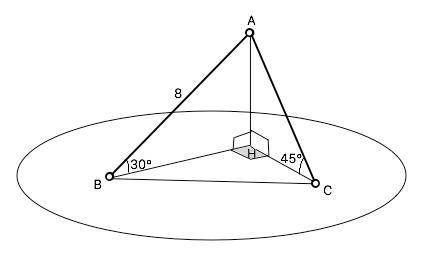
Из точки над плоскостью проведены две наклонные. Найдите расстояние между концами наклонных, если самая длинная наклонная - 8 см. Образующие с плоскостью углы равны 45° и 30°, а проекции наклонных между собой создают угол 90°.
Только очень прошу поподробнее! Заранее спасибо!

Ответ: 8 см

Объяснение:

  Пусть Н – проекция точки А на плоскость.

Наклонная АВ=8, угол АВН=30°; наклонная АС образует с плоскостью угол АСН=45°. Угол между проекциями наклонных ВНС=90°. Расстояние между концами наклонных -  ВС=?

АН перпендикулярен плоскости, ∆ АНС и АНВ - прямоугольные.

АН противолежит углу 30° и равен половине гипотенузы АВ.

АН=4 см.

Тогда ВН=АВ•cos30°=4√3 (или по т.Пифагора).

∆ АНС равнобедренный, т.к.  из суммы углов треугольника углы при АС равны. => НС=АН=4.

ВС по т. Пифагора=√(ВН²+СН²)=√48+16)=8 (см)