Предмет: Алгебра, автор: aleckkuz1

решите интеграл,сделаю лучшим ответом

Приложения:

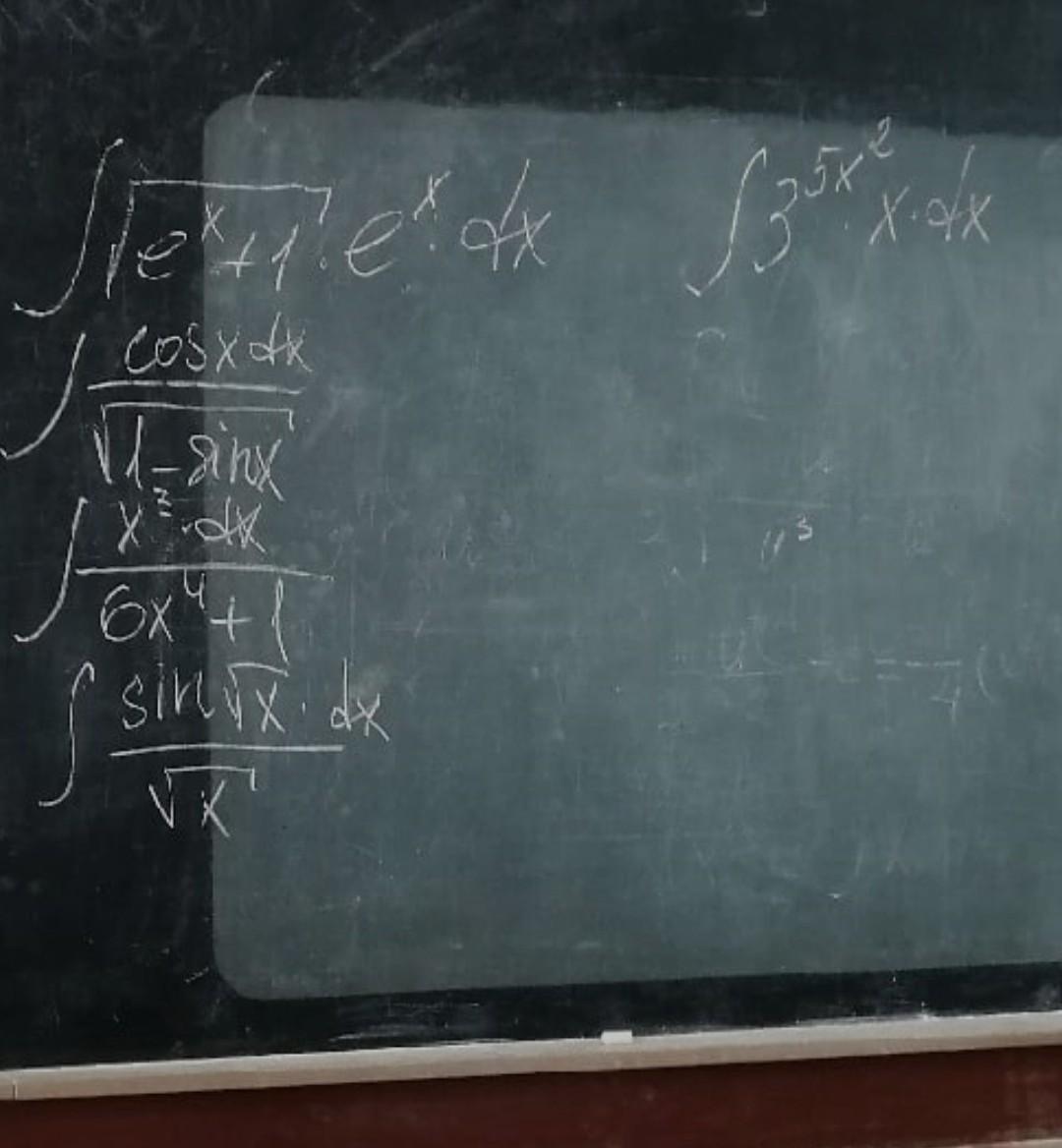
Ответы

Автор ответа: Miroslava227

2

Ответ:

1

$\int\limits \sqrt{1 + { e }^{x} } {e}^{x} dx = \int\limits \sqrt{1 + {e}^{x} } d(e {}^{x} ) = \\ = \int\limits {(1 + {e}^{x} )}^{ \frac{1}{2} } d(e {}^{x} + 1) = \frac{ {(1 + {e}^{x} )}^{ \frac{3}{2} } }{ \frac{3}{2} } + C = \\ = \frac{2}{3} \sqrt{ {(1 + {e}^{x}) }^{3} } + C$

2

$\int\limits \frac{ \cos(x) }{ \sqrt{1 - \sin(x) } } dx = \int\limits \frac{d( \sin(x)) }{ \sqrt{1 - \sin(x) } } = \\ = - \int\limits \frac{d(1 - \sin(x)) }{ {(1 - \sin(x)) }^{ \frac{1}{2} } } = \frac{ {(1 - \sin(x)) }^{ \frac{1}{2} } }{ \frac{1}{2} } + C = \\ = 2 \sqrt{1 - \sin(x) } + C$

3

$\int\limits \frac{ {x}^{3} }{6 {x}^{4} + 1} dx = \frac{1}{24} \int\limits \frac{24 {x}^{3}dx }{6 {x}^{4} + 1 } = \\ = \frac{1}{24} \int\limits \frac{d(6 {x}^{4} + 1)}{6 {x}^{4} + 1} = \frac{1}{24} ln( |6 {x}^{4} + 1 | ) + C$

4

$\int\limits \frac{ \sin( \sqrt{x} ) }{ \sqrt{x} } dx \\ \\ \sqrt{x} = t \\ \frac{1}{2 \sqrt{x} } dx = dt \\ \frac{dx}{ \sqrt{x} } = 2dt \\ \\ 2\int\limits \sin(t) dt = - 2 \cos(t) + c = \\ = - 2 \cos( \sqrt{x} ) + C$

5

$\int\limits {3}^{5 {x}^{2} } xdx = \frac{1}{10} \int\limits {3}^{5 {x}^{2} } \times 10xdx = \\ = \frac{1}{10} \int\limits {3}^{5 {x}^{2} } d(5 {x}^{2} ) = \frac{ {3}^{5 {x}^{2} } }{10 ln(3) } + C$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: megayazilya

Ребята помогите пожалуйста!. Поставьте глаголы, данные в скобках, в НУЖНОМ времени и переведите предложения на русский язык:
1. Yesterday my son (to have) two helpings of ice¬cream.
2. Last suirmer she (to stay) at our hotel.
3. How many helpings of sturgeon they (to ordee) ?
4. When they came to tables ( to be laid).
5. That day we (to go) to the restaurant after theatre.
6. I ... every other day (to work) .
7. This waiter ... 3 tables by the window (to serve).
8. Here your breakfast (to be).
9. you., in Moscow or outskirts (to live)?
10. When ... you ... more visitors in summer or in win¬ter (to have)?
11 Listen? The telephone (to ring).

2 года назад

Предмет: Русский язык, автор: Аноним

в каком слове 6 букв и 6 звуков? 1 письмо 2 сердце 3 листья 4 заехал

2 года назад

Предмет: Русский язык, автор: Чолалла

Учебная задача. Производите фонетический разбор слов. Определите количество звуков и букв в словах. Почему оно не совпадает?

2 года назад

Предмет: Химия, автор: annuwka89

К 500г.25 % раствору прибавили 500г. воды. Определить массовую долю растворенного вещества в новом растворе.

8 лет назад

Предмет: Русский язык, автор: irinabondarchik

Замените фразеологизм «одним словом»:
душа нараспашку, золотые руки, быть не из робкого десятка, светлая голова, Аника-воин,
ходячая энциклопедия, не к лицу, нос повесить, пускать пыль в глаза, стреляный воробей
(10 фразеологизмов).

8 лет назад