Предмет: Алгебра, автор: 0arti0

номер 1 решить систему неравенств.
номер 2 неравенства решить оба задания даю 16 баллов.

Приложения:

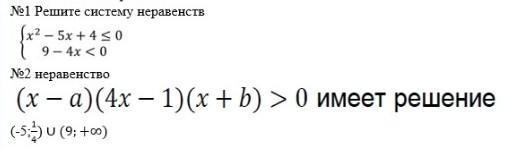
Ответы

Автор ответа: Miroslava227

0

Ответ:

1

$\left \{ {{x {}^{2} - 5x + 4 \leqslant 0 } \atop {9 - 4x < 0} } \right. \\ \\ 1) {x}^{2} - 5x + 4 \leqslant 0 \\D = 25 - 16 = 9 \\ x_1 = \frac{5 + 3}{2} = 4 \\ x_2 = 1 \\ + \: \: \: \: \: - \: \: \: \: \: \: \: \: \: + \\ - - 1- - 4 - - > \\ x\in[1;4] \\ \\ 2)9 - 4x < 0 \\ - 4x < - 9 \\ x > \frac{9}{4} \\ x > 2.25 \\$

При пересечении ответ:

$x\in(2.25;4]$

2.

$(x - a)(4x - 1)(x + b) > 0$

$4x - 1 = 0 \\ x = \frac{1}{4}$

Остались два числа: -5 и 9

$x - a = 0 \\ x = - 5\\ - 5 - a = 0 \\ a = - 5$

$x + b = 0 \\ x = 9\\9 + b = 0 \\ b = - 9$

Ответ: а = -5; б = -9

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: Аленагол

Как нарисовать символ добра

2 года назад

Предмет: Русский язык, автор: floryan05

Запиши имена существительные в Р.п множественного числа:
тысяча
встреча
зрелище
роща

2 года назад

Предмет: Немецкий язык, автор: gnatyukkarina

Помогите, пожалуйста!!!
Вставьте подходящий предлог, переведите предложения:
1. ...der Straßenecke fragte Jürgen ...Weg ...der Oper.

2 года назад

Предмет: Биология, автор: maxrashad

1. Ген- участок:
1) ядра; 2)ДНК; 3) хромосомы; 4) РНК
2. Наиболее развита корневая система у растений:
1) тенелюбивые;
2) водных;
3) сухих мест обитания;
4) избыточного увлажнения мест обитания;
3. углекислый газ при дыхании у человека образуется:
1) в лёгких;
2) в клетках тела;
3) в эритроцитах человека;
4) в воздушных путях;

8 лет назад

Предмет: Литература, автор: mikklikk

Срочно люди! Краткий пересказ рассказа Судьба человека М.А.Шолохова!!!

8 лет назад