СРОЧНО!!!!!!!! Помогите!!!!!!
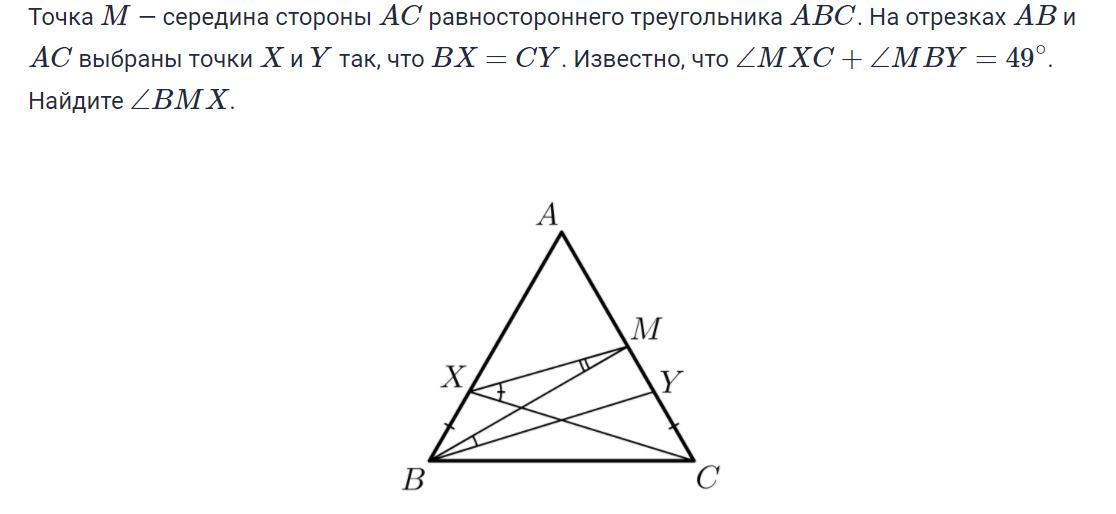
Точка M — середина стороны AC равностороннего треугольника ABC. На отрезках AB и AC выбраны точки X и Y так, что BX=CY. Известно, что ∠MXC+∠MBY=49∘. Найдите ∠BMX.

Ответ:

∠BMX=11°

Объяснение:

Дано: ΔАВС - равносторонний;

BX=CY

∠1=∠2=49°

Найти: ∠ВМХ

Решение:

1. Рассмотрим ΔВХС и ΔBYC.

XB=YC (условие)

ВС-общая

∠В=∠С=60° (ΔАВС - равносторонний)

⇒ ΔВХС = ΔBYC (1 признак)

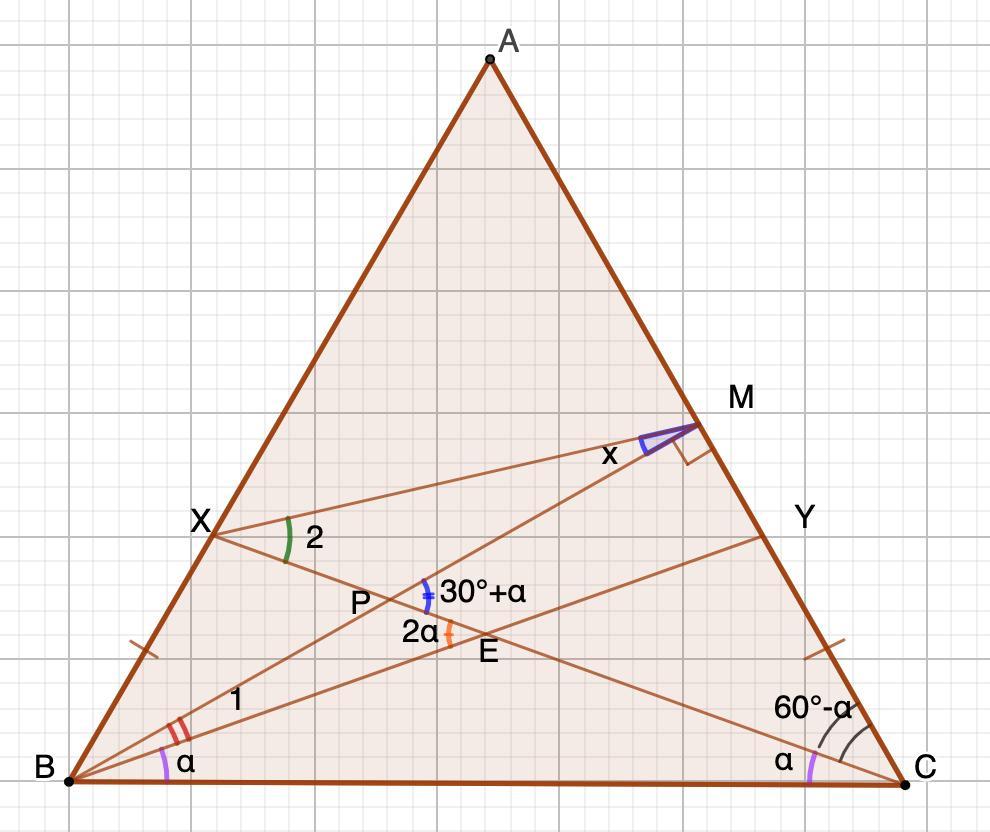
⇒ ∠YBC=∠XCB=α

2. ∠ХЕВ=2α (внешний)

3. Рассмотрим ΔСРМ -прямоугольный (ВМ - медиана, высота)

∠ЕСМ=60°-α ⇒ ∠СРМ=90°-(60°-α)=30°+α (сумма острых углов п/у Δ)

4. Рассмотрим ΔВРЕ

∠1+∠ВЕР=∠СРМ (внешний)

∠1+2α=30°+α ⇒ ∠1=30°-α

5. Рассмотрим ΔРХМ

∠2+х=∠СРМ (внешний)

∠2+х=30°+α ⇒ ∠2=30°+α-х

6. ∠1+∠2=49° (условие)

30°-α+30°+α-х=49°

60°-х=49°

х=11°