Предмет: Алгебра,
автор: Glanik34
Родные, докажите тождество пожалуйста.
Чего то совсем туплю
Приложения:
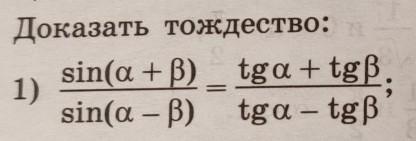
Ответы
Автор ответа:
2
Ответ:
См. Объяснение
Объяснение:
1) В числителе - синус суммы двух углов:
sin(α+β) = sinα·cosβ + cosα·sinβ
2) В знаменателе - синус разности двух углов:
sin(α-β) = sinα·cosβ - cosα·sinβ
3) Почленно разделим числитель и знаменатель на cosα·сosβ, в результате получим:
sinα·cosβ / cosα·сosβ = tgα
cosα·sinβ / cosα·сosβ = tgβ
4) Таким образом:
(sinα·cosβ + cosα·sinβ)/ (sinα·cosβ - cosα·sinβ) = (tgα +tgβ) /(tgα - tgβ) .
Следовательно:
sin(α+β)/sin(α-β) = (tgα +tgβ) /(tgα - tgβ) - что и требовалось доказать.
Glanik34:
мужчина!
просто мужик!
спасибо
не за что)))
Автор ответа:
1
распишем правую часть, помня, что tgt=sint/cost
((sinα/cosα)+(sinβ/cosβ))/((sinα/cosα)-(sinβ/cosβ))=
((sinα*cosβ+sinβ*cosα)/(cosα*cosβ))*((cosα*cosβ)/((sinα*cosβ+sinβ*cosα))=
sin(α+β)/sin(α-β) доказано.
Интересные вопросы
Предмет: Русский язык,
автор: aloqa21550
Предмет: Русский язык,
автор: ананасикYOUtube
Предмет: Русский язык,
автор: lolpa22
Предмет: Обществознание,
автор: Aleksandr191101
Предмет: Математика,
автор: Аноним