Из пункта А по одному шоссе выезжают одновременно два автомобиля, а через час вслед за ними выезжает третий. Еще через час расстояние между третьим и первым автомобилями уменьшилось в 1,5 раза, а между третьим и вторым - в 2 раза. Во сколько раз скорость первого автомобиля больше скорости второго, если известно, что третий автомобиль не обогнал первые два?

Внимательно прочитав условие, делаем вывод v₃ ≥ v₁ ≥ v₂ (где vₙ - скорость n-го автомобиля)

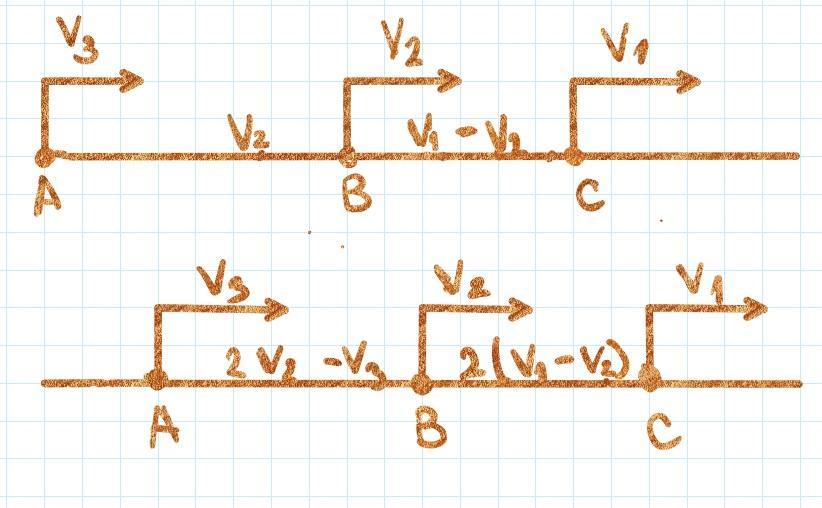
На рисунке - 2 схемы, 1-я соответствует моменту начала движения 3-го автомобиля, а 2-я - моменту через 1 час после начала движения 3-го.

На 1 схеме:

AB = v₂ (расстояние за 1 час, пройденное 2-м)

BC = v₁ - v₂ (расстояние между 1-м и 2-м через 1 час после начала движения)

AC = v₁

На 2 схеме:

AB = v₂ + v₂ - v₃ = 2v₂ - v₃

BC = 2(v₁ - v₂) = 2v₁ - 2v₂

AC = 2v₁ - v₃

По условию задачи:

AC (1 схема) в 1,5 раз больше AC (2 схема):

v₁ = 1,5·(2v₁ - v₃)

v₁ = 3v₁ - 1,5v₃

1,5v₃ = 2v₁

v₃ = 4/3 v₁

AB (1 схема) в 2 раза больше AB (2 схема):

v₂ = 2·(2v₂ - v₃)

v₂ = 4v₂ - 2v₃

3v₂ = 2v₃

v₃ = 3/2 v₂

Получаем, что 4/3 v₁ = 3/2 v₂

v₁ = 9/8 v₂

Ответ: скорость 1-го в 9/8 раз больше скорости 2-го