Предмет: Математика, автор: irishasvet79

Розв'яжіть нерівність у' >=0,якщо у=(х^2+3)/х+1

Ответы

Автор ответа: pushpull

Ответ:

Пошаговое объяснение:

$\displaystyle y' = \bigg (\frac{x^2+3}{x+1} \bigg )'=\frac{(x^2+3)'(x+1)-(x^2+3)(x+1)'}{(x+1)^2} =\frac{2x(x+1)-x^2-3}{(x+1)^2} =$

$\displaystyle =\frac{x^2+2x-3}{(x+1)^2}$

$\displaystyle \frac{x^2+2x-3}{(x+1)^2} \geq 0$

ОДЗ х ≠ -1 поскольку (х+1)² при х≠-1 всегда > 0, рассмотрим

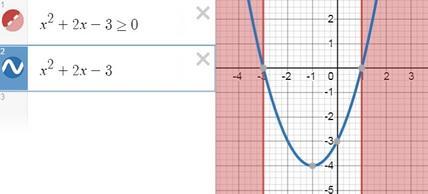
x² +2x -3 ≥ 0

x² +2x -3 = 0 ⇒ x1 = -3 x2 = 1 ⇒ x² +2x -3 ≥ 0 при х ∈ [-∞;-3] ∪[1; +∞]

т.к. -1 не попадает в отрезок, то

ответ

х ∈ [-∞;-3] ∪ [1; +∞]

Приложения:

irishasvet79: спасибо

irishasvet79: точно на этом промежутке у'>=0

irishasvet79: а с (х+1)^2 ничего не нужно делать?

irishasvet79: может быть (-~;-3) и (1;+~)?

pushpull: (х+1)^2 всегда >=0 т.к. это квадрат числа

pushpull: с прмежутком вы правы. тут я ошиблась. ветви параболы ввенрх, промежуток у вас правильный. попробую исправить ответ

Интересные вопросы

Предмет: Қазақ тiлi, автор: alena257

2 года назад

Предмет: Английский язык, автор: nargizcavid

2 года назад

Предмет: Русский язык, автор: elmira3005

2 года назад

Предмет: Математика, автор: BMSKRA

8 лет назад

Предмет: Математика, автор: Аноним

8 лет назад