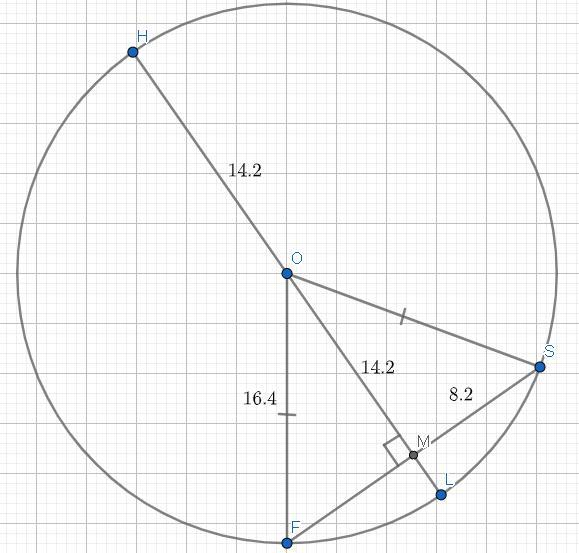
3. В окружности с центром в точке О к хорде SF, равной радиусу окружности, перпендикулярно проведен диаметр HL. Диаметр HL и хорда SF пересекаются в точке M.
Длина отрезка SM равна 8,2 см.
a) постройте рисунок по условию задачи;
b) определите длину хорды SF;
c) определите длину диаметра HL;
d) найдите периметр треугольника ОSF
Ответы
a)
В единственной картинке.
b)
Так как хорда SF — равна радиусу, то треугольник OFS, образованный двумя радиусами и хордой SF — правильный.
То есть:
HL — диаметр, перпендикулярный хорде SF, то есть: OM ⊥ SF.
То есть отрезок OM — высота, проведённая к основанию, а в правильном треугольнике, высота, биссектриса и медиана, проведённые к основанию — одно и то же.
То есть OM — медиана, что и означает, что:
Вывод: FS = 16.4см.
c)
Так как OM — высота треугольника OFS, проведённая к основанию, то треугольники OFM & OSM — прямоугольные, так как каждый из них имеет прямой угол (<OMF; <OMS).
OF — гипотенуза, FM — катет, чтобы найти второй катет, то есть OM, используем теорему Пифагора:
Диаметр равен половине отрезка OM, то есть:
Вывод: Диаметр HL равен 28.4см.
d)
Как я говорила ранее — треугольник OSF — правильный, то есть все стороны равны, то есть:
Вывод: Периметр треугольника OSF равен 49.2см.