Пожалуйста ответьте быстрее, мне нужно срочно!!! Отдам все свои баллы))
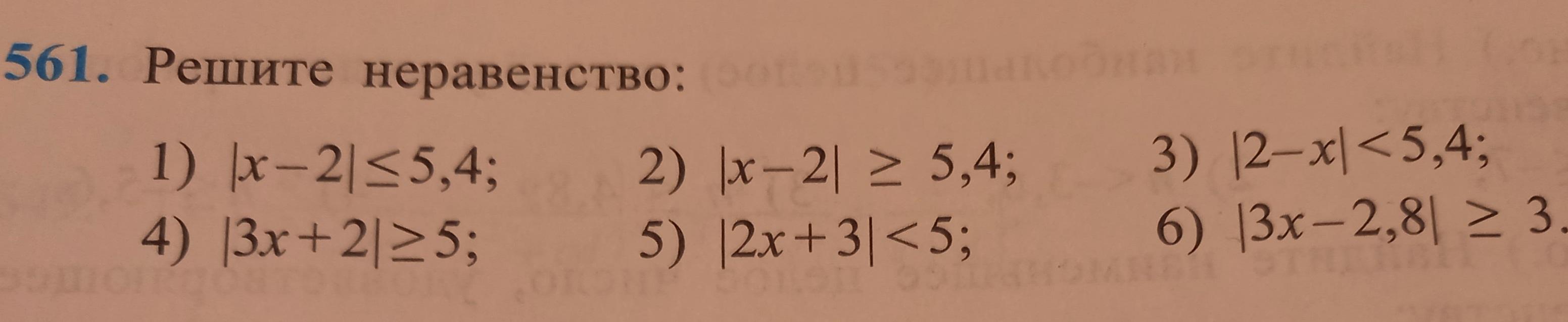
Ответы
Ответ:
В решении.
Объяснение:
Решить неравенства с модулем:
1) |x - 2| <= 5,4
х - 2 <= 5,4 x - 2 >= -5,4
x <= 5,4 + 2 x >= -5,4 + 2
x <= 7,4; x >= -3,4.
Решение неравенства: х∈[-3,4; 7,4].
2) |x - 2| >= 5,4
x - 2 >= 5,4 x - 2 <= -5,4
x >= 5,4 + 2 x <= -5,4 + 2
x >= 7,4; x <= -3,4.
Решение неравенства: х∈(-∞; -3,4]∪[7,4; +∞).
3) |2 - x| < 5,4
2 - x < 5,4 2 - x > -5,4
-x < 5,4 - 2 -x > -5,4 - 2
-x < 3,4 -x > -7,4
x > -3,4; x < 7,4.
Решение неравенства: х∈(-3,4; 7,4).
4) |3x + 2| >= 5
3х + 2 >= 5 3x + 2 <= -5
3x >= 5 - 2 3x <= -5 - 2
3x >= 3 3x <= -7
x >= 1; x <= -7/3.
Решение неравенства: х∈(-∞; -7/3]∪[1; +∞).
5) |2x + 3| < 5
2x + 3 < 5 2x + 3 > -5
2x < 5 - 3 2x > -5 - 3
2x < 2 2x > -8
x < 1; x > -4.
Решение неравенства: х∈(-4; 1).
6) |3x - 2,8| >= 3
3x - 2,8 >= 3 3x - 2,8 <= -3
3x >= 3 + 2,8 3x <= -3 + 2,8
3x >= 5,8 3x <= -0,2
x >= 1 и 14/15; x <= -1/15.
Решение неравенства: х∈(-∞; -1/15]∪[1 и 14/15; +∞).