Предмет: Геометрия, автор: gnbbbf

Помогите решить что-нибудь.​

Приложения:
gnbbbf: ну и на этом спасибо)
gnbbbf: ну если что то ещё сможешь, то был бы очень благодарен
gnbbbf: спасибо чк

Ответы

Автор ответа: Vopoxov
1

Объяснение:

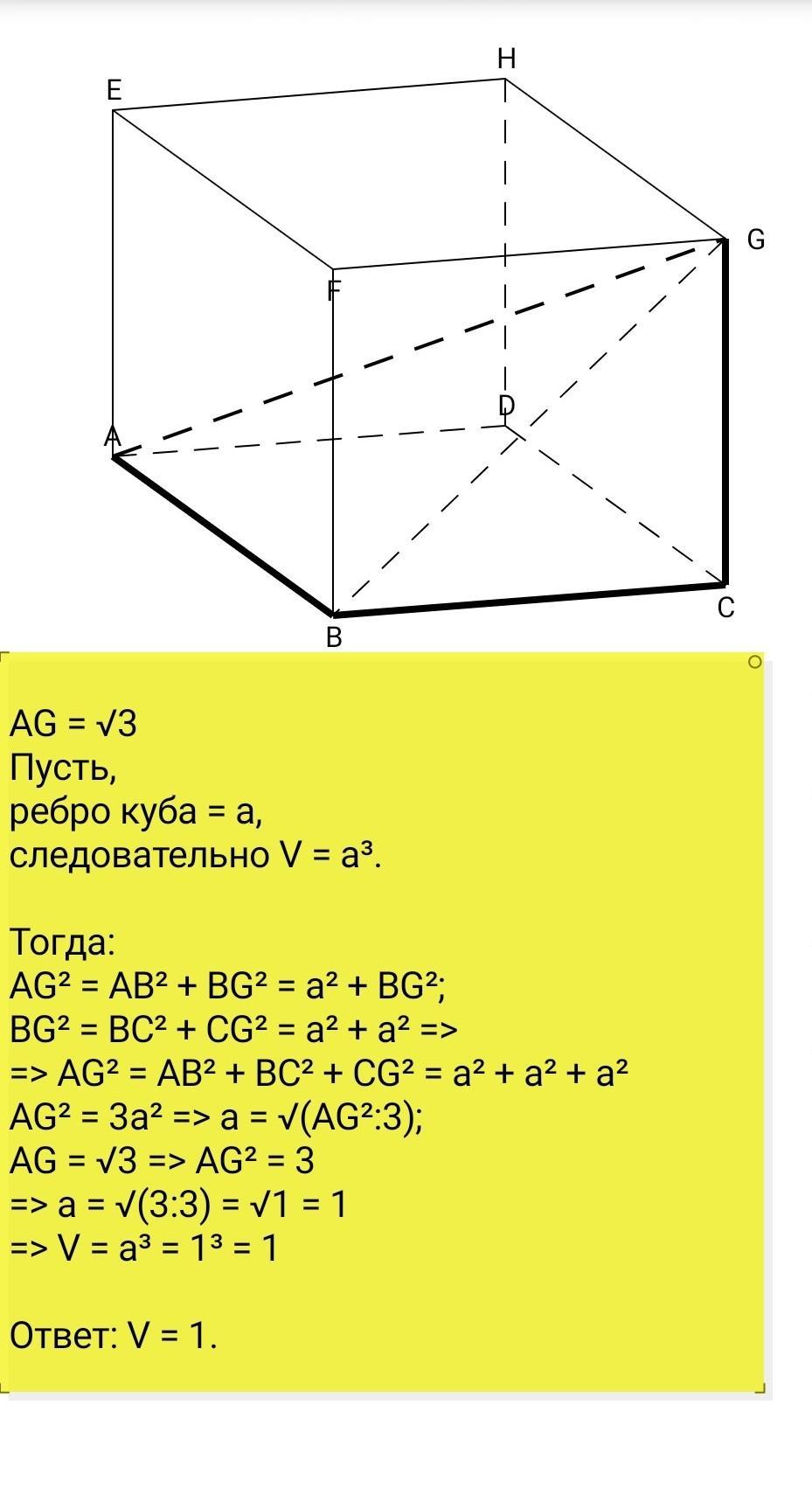
1. Дано: АВСDЕFGH - куб.

АG = √3 - диагональ

Найти: V(куба) = ?

Решение:

V(куба) = a³, где а - длина ребра куба.

Далее см. рис.

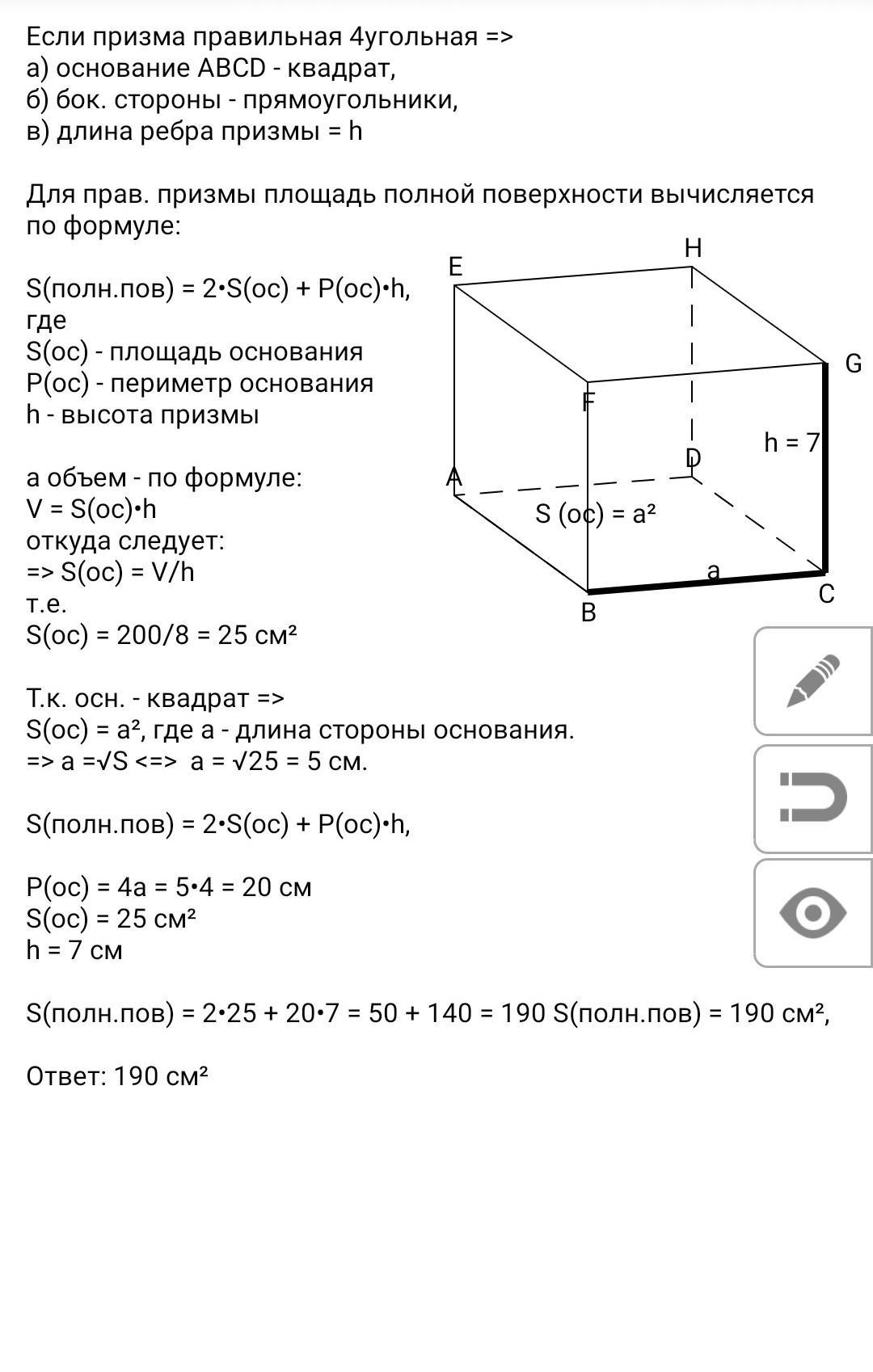
2. Дано:

АВСDЕFGH - прав. 4-угольн призма.

h = 8 см

V = 200 cm

Найти :

S(полн. пов) = ?

Ответ: 190 см²

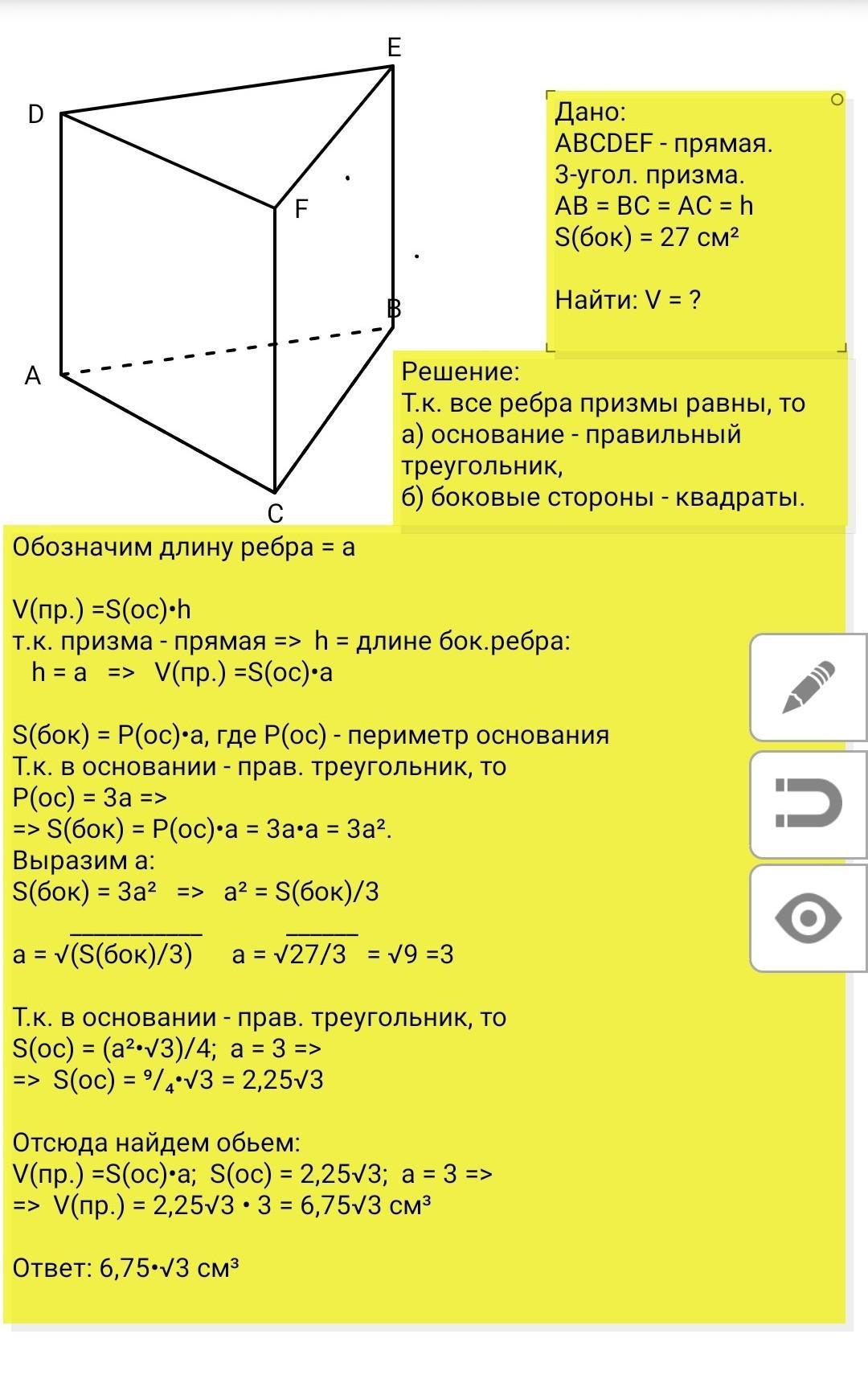
3. Дано: ABCDEF - прям. треуг. призма.

АВ = ВС = АС = h.

S(бок) = 27 см²

Найти: V(пр.) = ?

Решение - см. рис.

Ответ: V = 6,75√3 см³

4. Дано:

.....

5. Дано:

V\small{_{шара} }= \frac{500}{3}\cdot\pi

Найти:

S\small{_{пов.\:ш.} }= ?

Решение: Обьем шара вычисляется по формуле:

V\small{_{шара} }= \frac{4}{3}\cdot\pi\cdot{R^3} , где R - радиус шара.

Преобразуем:

V\small{_{шара} }= \frac{4}{3}\cdot\pi{\cdot}R^3 <=> \frac{3}{4}V\small{_{шара} }= \pi{\cdot}R^3<=> \\\frac{ \frac{3}{4}V\small{_{шара} }}{\pi}=R^3 \: <=>R= \sqrt[3]{\frac{ \frac{3}{4}V\small{_{шара} }}{\pi} } <=>R= \sqrt[3]{\frac{3V\small{_{шара} }}{4\pi} }

R= \sqrt[3]{\frac{3V\small{_{шара} }}{4\pi} }; \: V\small{_{шара} }= \frac{500\pi}{3}\\R= \sqrt[3]{\frac{3\cdot\frac{500\pi}{3}}{4\pi} }\\ R= \sqrt[3]{\frac{500}{4}}=\sqrt[3]{125} = \sqrt[3]{5^3}= 5 \: cm

Найдем пл. пов.:

S\small{_{пов.\:ш.} }= 4\pi\cdot{R^2}; \: \: \: R = 5 => \\ => S\small{_{пов.\:ш.} }= 4\pi\cdot{5^2}=4\pi\cdot{25}=100\pi \: cm^2

Ответ: 100\pi\:\: cm^2

Приложения:
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Английский язык, автор: ksenyakarpova
1) There a) is a telegram for you.
b) are
с) were
2) There a) was no lectures yesterday.
b) were
с) are
3) Is there a) some flights for London today?
b) any flights
с) a flight
4) There a) is mush snow last winter.
b) was
с) were
5) We are going to buy a) something cheese.
b) some
с) no
6) She can’t pay for education, she has a) something money.
b) some
с) no
7) There are a) some people in the room. It is empty.
b) few
с) no
8) Is there any water in the cattle? – a) No, there isn’t any.
b) No, there is any.
с) No, there is no.
9) Did you see a) somebody in the street? – No, I didn’t.
b) anybody
с) some
10) There a) is many places of interest in London.
b) are
с) was
11) В моей библиотеке нет никаких немецких книг.
a) There aren’t any German books in my library.
b) There are no German books in my library.
с) There are nothing German books in my library.
12) Translate into English
а) В нашем колледже есть семь отделений.
б) В столовой есть много вкусных блюд.
в) В неделе семь дней./ There are 7 days in a week.
г) На прошлой неделе не было ни одной лекции.
д) Был вчера в программе какой-нибудь интересный концерт?
2 года назад
Предмет: Русский язык, автор: Ae230705
Наверху вместе наоборот вначале записать словочитание
2 года назад
Предмет: Русский язык, автор: лера463
большая вишня как часть речи разобрать
2 года назад
Предмет: Биология, автор: nikvoropaev77
водоросли мхи пожалуйста нужно срочно!!!!!!!!!!!!!!!!!!!!!!!!!!
8 лет назад
Предмет: Алгебра, автор: Fozkorrr
Одна на сторон прямоугольника на 7 см больше другой , а его диагональ равна 13 см . Найдите стороны прямоугольника .
8 лет назад