Предмет: Алгебра,
автор: vorobej527
Доведите Тотожность, на фото 17.31
Приложения:
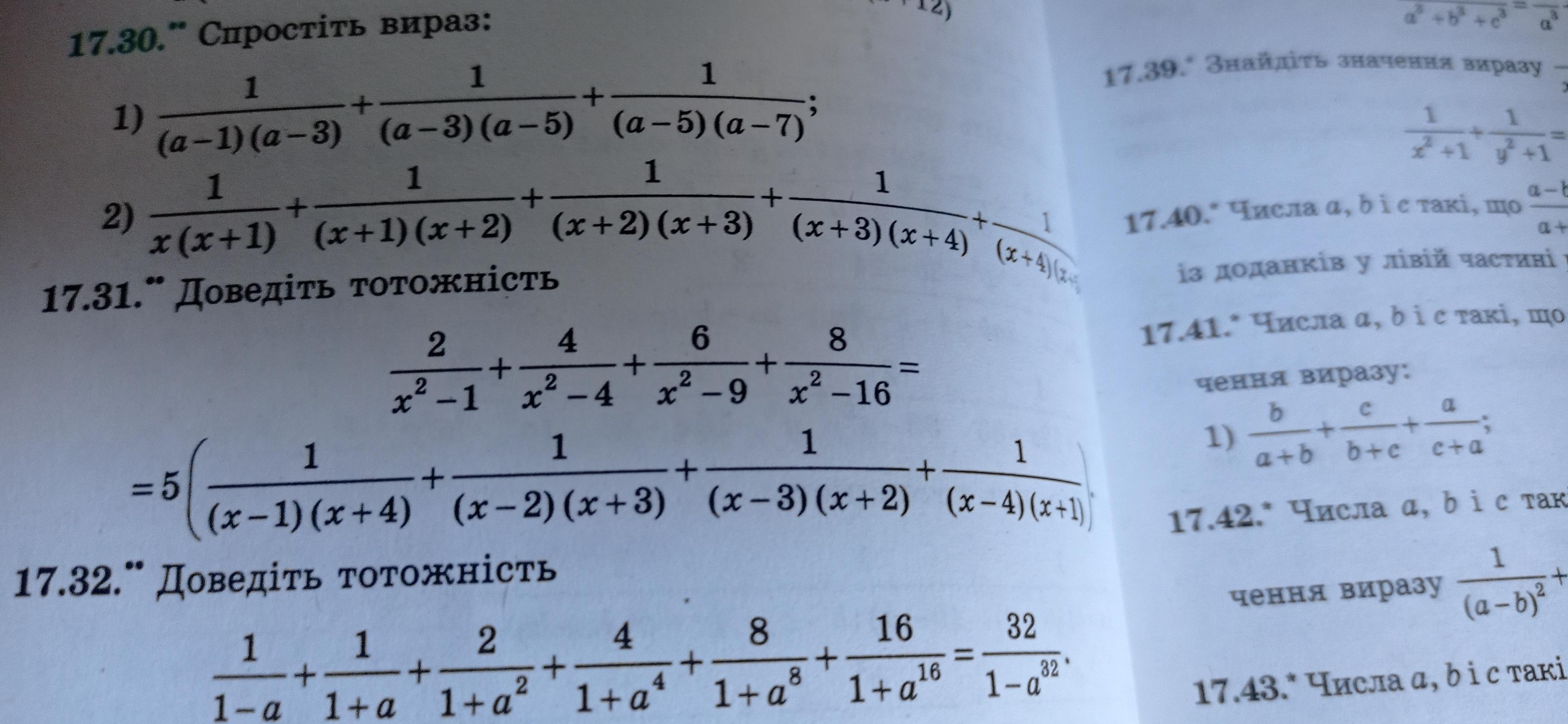
Ответы
Автор ответа:
0
Интересные вопросы
Предмет: Английский язык,
автор: olezhkakudinov
Предмет: Окружающий мир,
автор: Аегршм7нгп
Предмет: Русский язык,
автор: толик46
Предмет: Химия,
автор: Aleksejklv
Предмет: Химия,
автор: rara24g