Предмет: Алгебра, автор: master920

Помогите пожалуйста, !!!!!

Приложения:

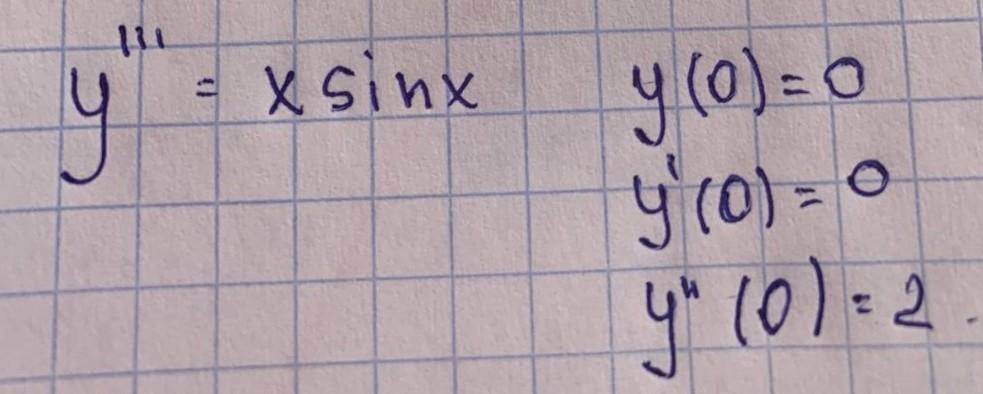
Miroslava227: в задачи Коши слишком много условий

Miroslava227: должно быть две пары

Miroslava227: обычно у(_)=_, у'(_)=_

master920: ну не знаю, такая задача, надо решить а нашёл y'''= xsinx а дальше не знаю что делать

Miroslava227: все, окей

Ответы

Автор ответа: Miroslava227

Ответ:

решение на фотографии.

Приложения:

NNNLLL54: В первой производной потеряли интеграл от sinx

Автор ответа: NNNLLL54

Ответ:

$y'''=x\cdot sinx\ \ ,\ \ y(0)=0\ ,\ y'(0)=0\ ,\ y''(0)=2\\\\\\y''=\int \underbrace{x}_{u}\cdot \underbrace{sinx\, dx}_{dv}=\Big[\ du=dx\ ,\ v=-cosx\ \Big]=uv-\int v\, du=\\\\=-x\cdot cosx+\int cosx\, dx=-x\cdot cosx+sinx+C_1;\\\\\\y'=\int (-x\cdot cosx+sinx+C_1)\, dx=-\int \underbrace{x}_{u}\underbrace{\cdot cosx\, dx}_{dv}+\int sinx\, dx+C_1\int dx=\\\\={}\Big[\ du=dx\ ,\ v=sinx\ \Big]=-\Big(x\cdot sinx-\int sinx\, dx\Big)-cosx+C_1x+C_2=\\\\=-x\cdot sinx-cosx-cosx+C_1x+C_2=-x\cdot sinx-2\, cosx+C_1x+C_2;$

$y=\int (-x\cdot sinx-2cosx+C_1x+C_2)\, dx=\\\\=-\int x\cdot sinx\, dx-2\int cosx\, dx+C_1\int x\, dx+C_2\int dx=\\\\=-\Big(-x\cdot cosx+sinx\Big)-2sinx+C_1\cdot \dfrac{x^2}{2}+C_2x+C_3=\\\\=x\cdot cosx-sinx-2sinx+C_1\cdot \dfrac{x^2}{2}+C_2x+C_3=\\\\=x\cdot cosx-3sinx+C_1\cdot \dfrac{x^2}{2}+C_2x+C_3\ ;$

$y_{obshee}=x\cdot cosx-3sinx+C_1\cdot \dfrac{x^2}{2}+C_2x+C_3\ ;$

$y(0)=0:\ \ \ 0=0\cdot cos0-3\, sin0+C_1\cdot 0+C_2\cdot 0+C_3\ \ ,\ \ C_3=0\\\\y''(0)=0:\ \ 0=-0\cdot sin0-2\, cos0+C_1\cdot 0+C_2\ ,\ \ 0=-2+C_2\ ,\ C_2=2\\\\y''(0)=2:\ \ 2=0\cdot cos0+sin0+C_1\ \ ,\ \ 2=C_1\ \ ,\ \ C_1=2\\\\\\\boxed{\ y_{chastnoe}=-x\cdot cosx-3\, sinx+x^2+2x\ }$