Предмет: Алгебра, автор: vysokylesha

Помогите решить пожалуйста

Приложения:

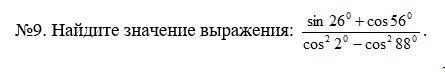
Ответы

Автор ответа: sangers1959

0

Объяснение:

$\frac{sin26^0+cos56^0}{cos^22^0-cos^288^0}=1 .$

Упростим числитель:

$sin26^0+cos56^0=sin26^0+sin(90^0-56^0)=sin26^0+sin34^0=sin34^0+sin26^0=\\=2*sin\frac{34^0+26^0}{2}*cos\frac{34^0-26^0}{2}=2*sin30^0*cos4^0.$

Упростим знаменатель:

$cos^22^0-cos^288^0=(cos2^0+cos88^0)*(cos2^0-cos88^0)=\\=(co88^0+cos2^0)*(cos2^0-cos88^0)=2*cos45^0*cos43^0*2*sin45^0*sin43^0=\\=2*\frac{\sqrt{2} }{2} *cos43^0*2*\frac{\sqrt{2} }{2}*sin43^0=4*\frac{1}{2} *sin43^0*cos43^0=\\=2*sin43^0*cos43^0=sin86^0=sin(90^0-4^0)=cos4^0. \ \ \ \ \Rightarrow$

$\frac{cos4^0}{cos4^0} =1.$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: FairyTail2103

таять какое это спряжение

2 года назад

Предмет: Русский язык, автор: echtyn

Объясните в чем сходство и различие слов пошел, пришел, прошел, отошел, пришел, вошел, шел

2 года назад

Предмет: Английский язык, автор: Виктория1801

помогите правильно поставить артикли

2 года назад

Предмет: Математика, автор: Liza0065V

Решите задачку плиз
В 1О часов утра на стадионе было 28 человек, из которых часть играли в футбол, а часть в волейбол. Затем 7 из игравших в футбол ушли со стадиона, а 3 человека игравших в волейбол, пошли играть в футбол. В результате игравших в футбол стало в 2 раза больше чем играющих в волейбол. Сколько человек играли в футбол в 1О часов утра?

8 лет назад

Предмет: Окружающий мир, автор: MaksimX32X32

расскажи о каком либо животном обитающем в твоём ригионе
Дикое животное я живу в Брянске

8 лет назад