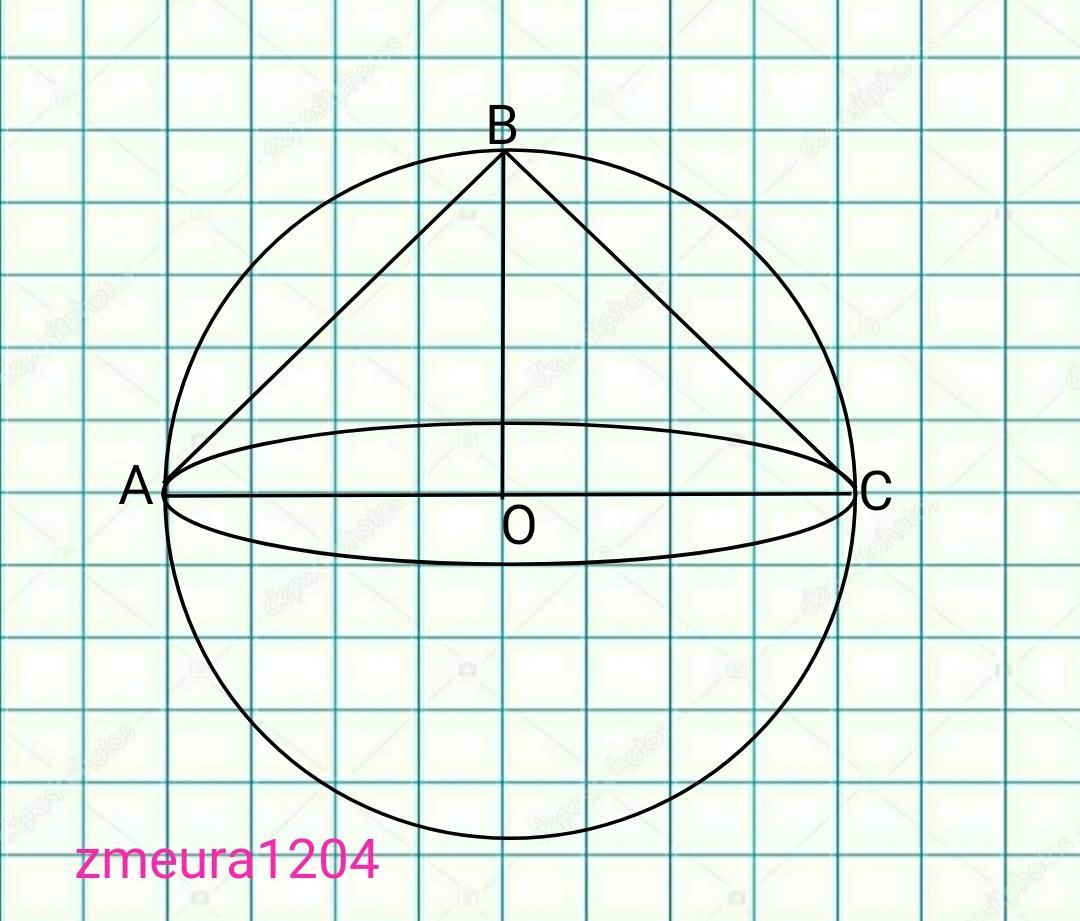
Объем шара равен 288 п . Найдите площадь боковой поверхности конуса, вписанного в шар. Основанием конуса является больший круг.

Ответ:

36√2π

Пошаговое объяснение:

V=4πR³/3

R=³√(3*V/4π)=³√(3*288π/4π)=³√216=6 радиус шара и радиус конуса

ОС=6

АС=2*ОС=2*6=12 диаметр конуса.

∆ABC- прямоугольный равнобедренный треугольник. <АВС- опирается на диаметр.

ВС=АС/√2=12/√2=6√2 образующая конуса.

Sбок.ц=π*R*L=π*OC*BC=π*6*6√2=36π√2

Ответ:

36π√2.

Пошаговое объяснение:

Vшара=4/3*π*R³

288π=4/3*π*R³ , R³=288*3/4=216=6³ ⇒R=6

R шара  совпал с r конуса тк основанием конуса является больший круг. S бок.конуса =πrL.

Образующуую конуса ищем из прямоугольного треугольника , где катеты R=6

L=√(6²+6²)=6√2

S бок.конуса =π*6*6√2=36π√2.