Предмет: Алгебра,
автор: polinaholi49
помогите пожалуйста, даю 35 баллов!!!!!!
Приложения:
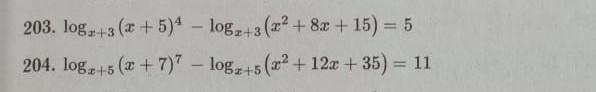
Ответы
Автор ответа:
1
Ответ:
Объяснение:
203.
x∈(-∞; -5) ∪ (-3; ∞)
OD3: (-3; ∞)
x≠ -4 тогда х= -1
204.
x∈(-∞; -7) ∪ (-5; ∞)
OD3: (-5; ∞)
x= -3
Интересные вопросы
Предмет: Русский язык,
автор: МашаШудрова
Предмет: Русский язык,
автор: Айка1985
Предмет: Русский язык,
автор: укцукцу
Предмет: Литература,
автор: Ирчик666
Предмет: Русский язык,
автор: kogoto123