Предмет: Математика, автор: noktoi

Помогите решить уравнение

Приложения:

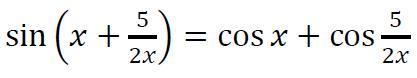
Ответы

Автор ответа: amanda2sempl

sin(x + 5/2x) = cosx + cos(5/2x) ⇔

2sin(x/2 + 5/4x)cos(x/2 + 5/4x) = 2cos(x/2 + 5/4x)cos(x/2 - 5/4x) ⇔

cos(x/2 + 5/4x)·(sin(x/2 + 5/4x) - cos(x/2 - 5/4x)) = 0 ⇒

cos(x/2 + 5/4x) = 0 or sin(x/2 + 5/4x) - cos(x/2 - 5/4x) = 0

a) cos(x/2 + 5/4x) = 0 ⇒ x/2 + 5/4x = π/2 + πk, k∈Z ⇒

2x² - 4x(π/2 + πk) + 5 = 0, D = 4²(π/2 + πk)² - 4·2·5 = 16(π/2 + πk)² - 40,

D ≥ 0 ⇒ 16(π/2 + πk)² - 40 ≥ 0 ⇒ (π/2 + πk)² ≥ 2,5 ⇒ |π/2 + πk| ≥ √2,5,

k∈Z ⇒ - √2,5 ≤ π(1/2 + k) ≤ √2,5 ⇒ - 0,5 - √2,5/π ≤ k ≤ - 0,5 + √2,5/π

√2,5/π ≈ 0,503 ⇒ -1,003 ≤ k ≤ 0,003 ⇒ k = {-1;0}. Тогда х = (4(π/2 + πk) ± (16(π/2 + πk)² - 40)^0,5)/4 = π/2 + πk ± ((π/2 + πk)² - 2,5)^0,5; для k = {-1;0} имеем: х₁₂ = (k = 0) = π/2 ± ((π/2)² - 2,5)^0,5,

х₃₄ = (k = - 1) = - π/2 ± ((π/2)² - 2,5)^0,5

б) sin(x/2 + 5/4x) - cos(x/2 - 5/4x) = 0 ⇒

cos(π/2 - x/2 - 5/4x) - cos(x/2 - 5/4x) = 0 ⇒

- 2sin(π/4 - 5/4x)·sin(π/4 - x/2) = 0 ⇒ sin(π/4 - 5/4x) = 0 or sin(π/4 - x/2) = 0.

1) sin(π/4 - 5/4x) = 0 ⇒ π/4 - 5/4x = πm, m∈Z ⇒

1/x = π(1 - 4m)/5 ⇒ x = $\frac{5}{\pi (1-4m)}$