Предмет: Геометрия,
автор: bkzdkin9
найдите площадь прямоугольного равнобедренного треугольника описанного около окружности радиуса √2
Ответы
Автор ответа:
2
см фото,,,,,,,,,,,,,,,,,,,,,
Приложения:
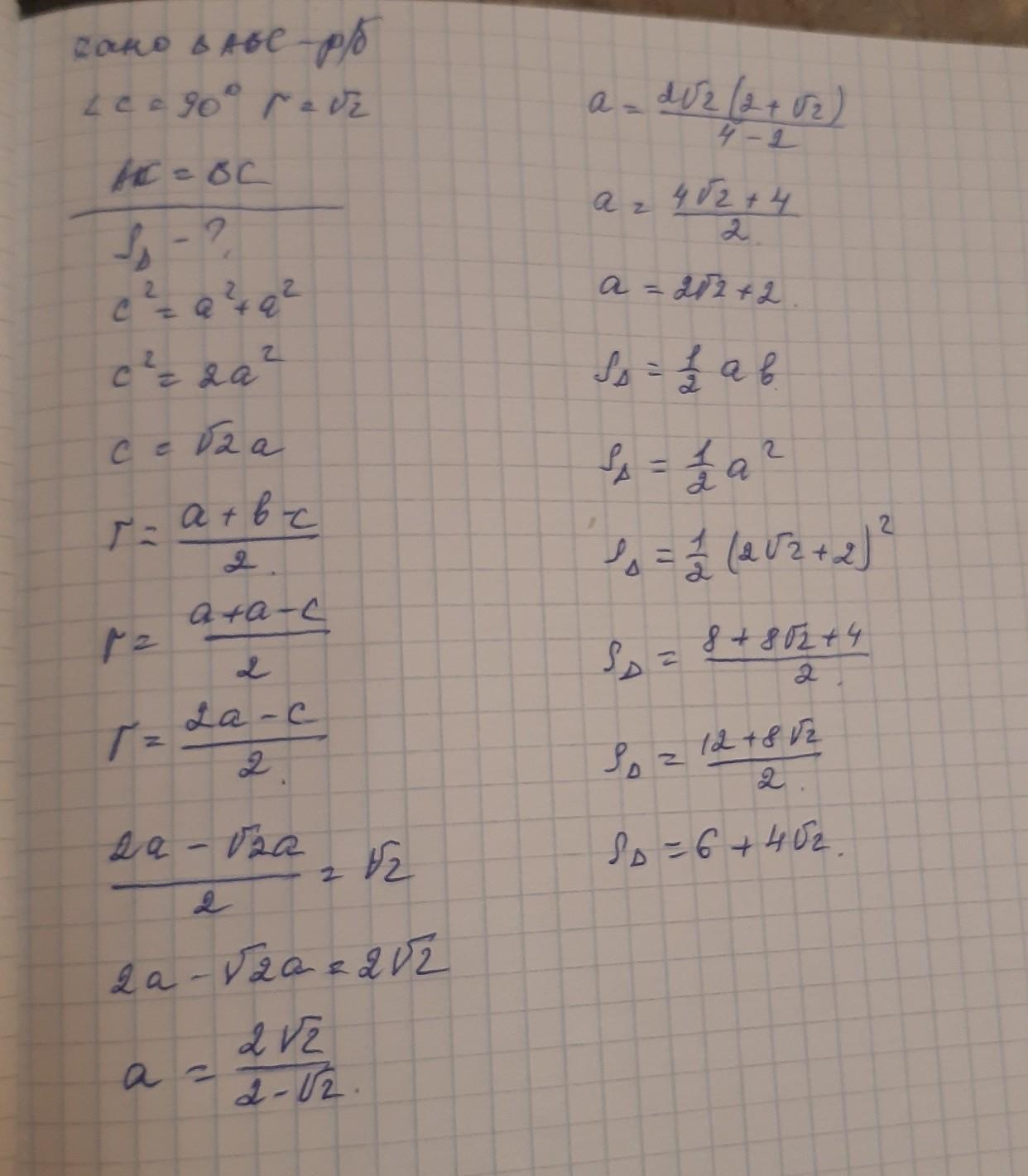
Автор ответа:
2
Ответ: 6+4√2 (ед. площади)
Вариант решения:
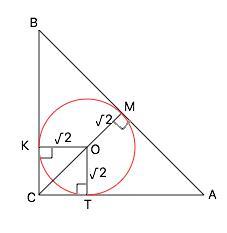
Центр вписанной в треугольник окружности лежит на биссектрисе. СМ - биссектриса, но и высота и медиана равнобедренного прямоугольного ∆ АВС. По свойству медианы прямоугольного треугольника
СМ=ВМ=АМ.
Точки К, Т, М - точки касания окружности со сторонами треугольника.
КОТС - квадрат со сторонами r=√2 =>
угол ОСТ=45°
Диагональ СО =КО:sin45°=√2:1/√2=2
СМ=СО+ОМ=2+√2
АВ=2 СМ=2(2+√2)
Ѕ(АВС)=СМ•АВ:2=(2+√2)•(2+√2)
Ѕ(АВС)=(2+√2)²=4+4√2+2=6+4√2 .
Приложения:
Интересные вопросы
Предмет: Английский язык,
автор: Чикади
Предмет: Английский язык,
автор: Teymur25
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: Zozerope