Предмет: Алгебра, автор: Reqiuem10

Я что-то не вырубаюсь где я допустил ошибку ?

Приложения:

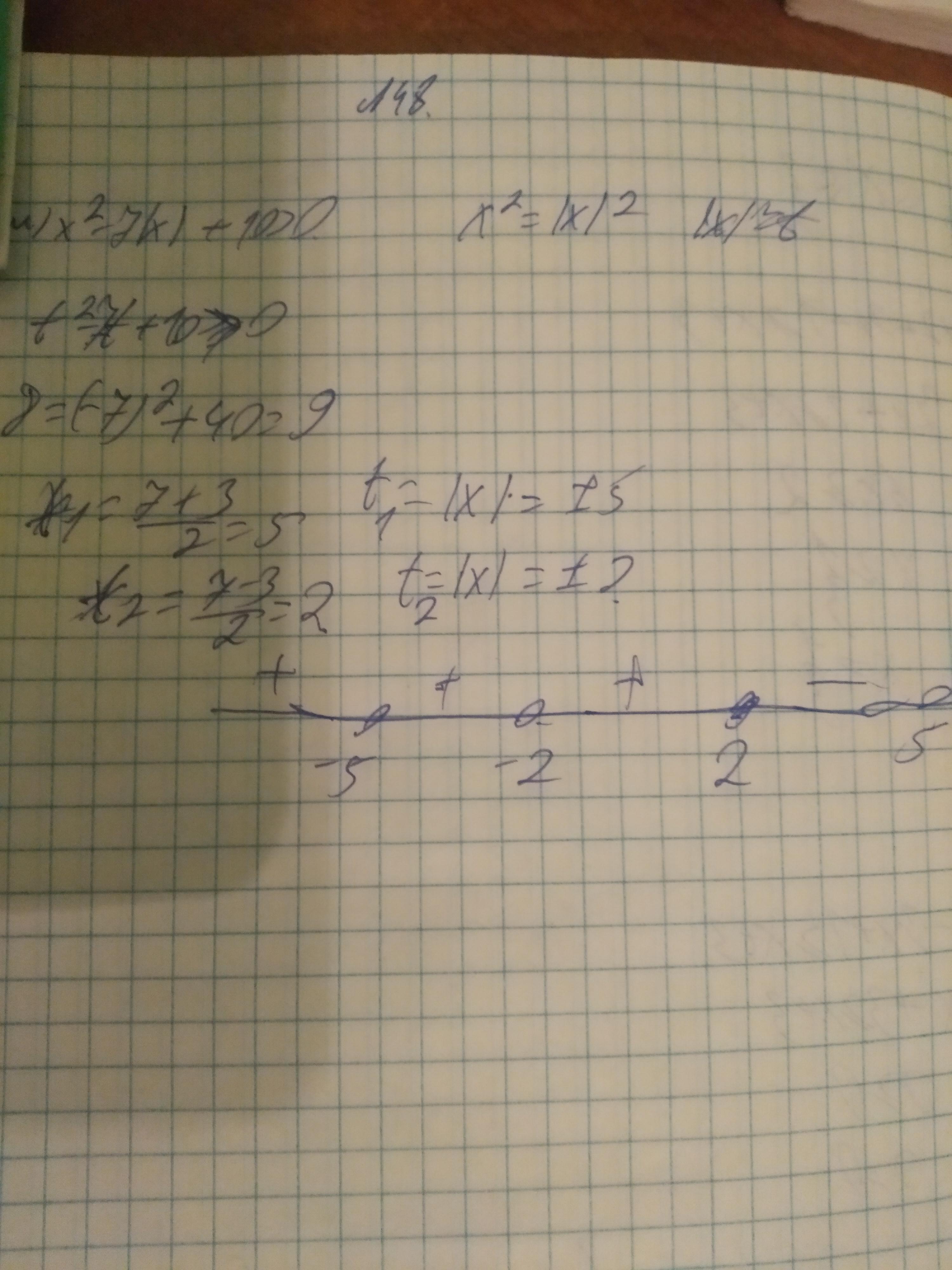
Ответы

Автор ответа: vlad97ua

0

$x^2-7|x|+10>0\\|x|^2-7|x|+10>0\\|x|=t, t\geq 0\\t^2-7t+10>0\\(t-2)(t-5)>0\\$\left[ \begin{gathered} t>5 \\ t<2 \\ \end{gathered} \right.$\\$\left[ \begin{gathered} |x|>5 \\ |x|<2 \\ \end{gathered} \right.$\\$\left[ \begin{gathered} x>5 \\ x<-5 \\ -2<x<2 \\ \end{gathered} \right.$\\$

Ответ: $x\in (-\infty;-5)\cup(-2;2)\cup(5;+\infty)$

matilda17562: Извините, решение не открывалось.

Автор ответа: MrSolution

0

Ответ:

(см. объяснение)

Объяснение:

$x^2-7|x|+10>0\\x^2-5|x|-2|x|+10>0\\|x|(|x|-5)-2(|x|-5)>0\\(|x|-5)(|x|-2)>0,\;<=>\;(x-5)(x+5)(x-2)(x+2)>0\\x\in(-\infty;\;-5)\cup(-2;\;2)\cup(5;\;+\infty)$

Задание выполнено!

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: японская69школьница

я поскорее поставил санки и побежал к друзьям. - проведите синтаксический разбор предложения

2 года назад

Предмет: Русский язык, автор: 110484

писать 10 слов существительные и определить их ж.р,м.р,с.р.

2 года назад

Предмет: Русский язык, автор: Викусякрасотуся

Укажите верное объяснение написания слова р..стение
1)пишется А,так как эта буква стоит перед СТ
2)пишется О,так как это слово-исключение
3)пишется А,так как это безударная гласная
4)пишется О,так как можно проверить словом рост

2 года назад

Предмет: Математика, автор: Keti3007

помогите,пожалуйста!)
зарание большое спасибо)))

8 лет назад

Предмет: Математика, автор: DEN22848

Срочно! Даю 12 балов! На одній полиці було в 3 рази більше книжок,ніж на другій. Коли з першої полиці зняли 30 книжок,а на другу поставили 10, то на обох полицях стало порівную. Скільки книжок було на кожній полиці спочатку?

8 лет назад