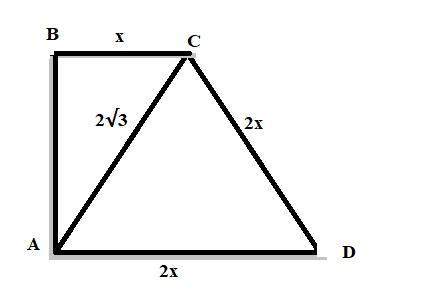
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, AC = 2√3. Найди периметр трапеции.​

Ответ:  ≈11.66.

Объяснение:

Решение.

По условию треугольник ACD - равнобедренный:

Если ВС=х, то AD=CD=2x/

Угол при вершине (угол D) равен 60°.

∠CAD=∠ACD=60°/ Следовательно ΔACD-равносторонний со сторонами равными 2√3.

По условию AD=2x;  ВС=х.  Тогда

ВС=1/2AD;

ВС=1/2*2√3;

ВС=√3.

------------------

По построению получается, что трапеция Прямоугольная (См. скриншот).

Находим сторону АВ:

Из прямоугольного треугольника АВС по т. Пифагора

АВ²=АС²-ВС²=(2√3)²-(√3)²=12-3=9;

АВ=√9=3.  Тогда периметр трапеции

P=AB+BC+CD+AD=3+√3+2√3+2√3=3+5√3≈11.66.