Предмет: Геометрия, автор: Аноним

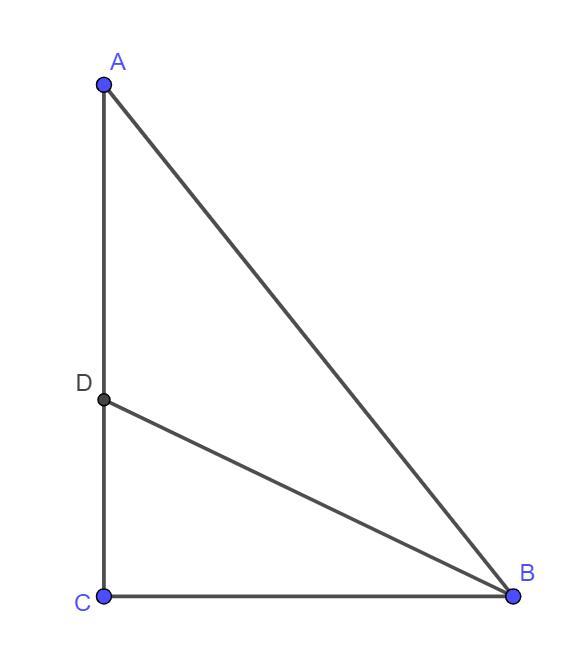
ПОМОГИТЕ ПОЖАЛУЙСТА . биссектриса острого угла прямоугольного треугольника АВС делит катет на отрезки равные 10см и 26 см. найдите площадь треугольника.

Simba2017: свойство биссектрисы же есть

Simba2017: (10x)^2+36^2=(36x)^2

cos20093: Это Пифагоров треугольник, подобный (5,12,13), с катетом 36, то есть коэффициент подобия 3; значит площадь (5*12/2)*3^2 = 30^9 = 270;

cos20093: 30*9 :)))) не степень, конечно

Аноним: даа всем спасибо решила другим способом

Ответы

Автор ответа: Аноним

1

По свойству биссектрисы: CD/AD = BC/AB

10/26 = BC/AB ⇒ BC/AB = 5/13 = sin A

С другой стороны BC/AB = cos B, тогда, используя основное тригонометрическое тождество, получаем

$\sin B=\sqrt{1-\cos^2B}=\dfrac{12}{13}=\dfrac{AC}{AB}$

Но так как AC = 26 + 10 = 36 см, то $\dfrac{AC}{AB}=\dfrac{12\cdot3}{13\cdot3}=\dfrac{36}{39}$ откуда AB = 39 см

S = 1/2 * AC * AB * sin A = 1/2 * 36 * 39 * 5/13 = 270 см²

Приложения:

Аноним: СПАСИБО

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: Аноним

как правильно пишится почуем или почуим. отдельное слово без предложения помогите

2 года назад

Предмет: Русский язык, автор: danila1296

Помогите разобрать предложение синтаксический разбор предложения
Порой в бору стоят одни лишь старые сосны. Там выделить подлежащее

2 года назад

Предмет: Английский язык, автор: xlebic2008

Помогите пожалуйста!!! Нужно перевести и вставить недостоющие слова! Заранее спасибо!
Dear granny! Thank you for your letter. I am happy that you are ok. We are all right, too. I would like to write you about Russian schools.
Russian children go to ... on the first of September. They have holidays in November, January and March. Summer ... are the longest. Lessons start at 8:30. Children from 7 to 10 go to Primary Schools. They usually have 5 or 6 ... every day.They are a lot of interesting ... ontheir timetable: Russian and English, Maths and Reading, Nature Study and Computing, Art and Music, Dancing and Sports.
In Russia ... are usually over at about 3 o*clock. After school children usually play games, go for a ... or to the swimming pools. Then they do their homework and read books.
Yesterday, I visited Masha*s school. Her classroom is very nice and comfortable. I liked their new desks, the teacher*s table and a large ... with a lot of wonderful books in it. Masha*s teacher is very clever and kind. She tells the children a lot of interesting things. Masha is very good ... English. It is her favourite ... . But she has some problems with Maths, because it*s difficult for her to do sums. I think I ... help her with Maths. You know, it*s favourite subject.
Please write to me soon.
Best wishes, Ann.

2 года назад

Предмет: Математика, автор: tiktak2018

два мальчика шли навстречу друг другу с одинаковой скоростью один до встречи шел 5 минут и прошёл на 130 м больше другого который был в пути 3 минуты Какое расстояние было между мальчиками сначаладва мальчика шли навстречу друг другу с одинаковой скоростью

8 лет назад

Предмет: Биология, автор: Marray3

К типичным формам приобретенного поведения относят

8 лет назад