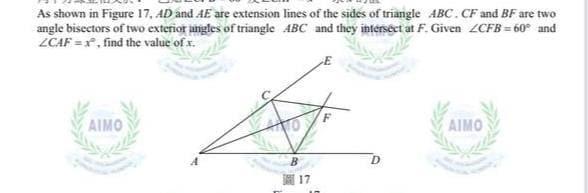
На рисунке 17 . AD и AE являются продолжениями сторон треугольника ABC . CF и BF это биссектрисы двух внешних углов треугольника ABC ; и они пересекаются в точке F . Если ∠CAF =x ; найдите величину угла x

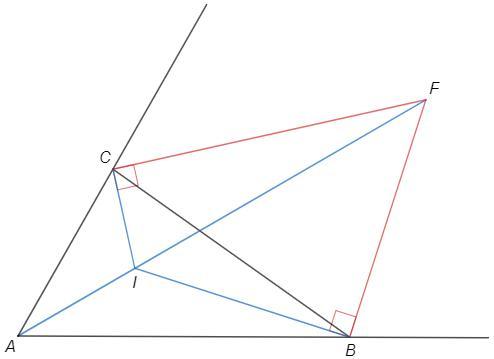
Биссектрисы двух внешних и внутреннего угла пересекаются в одной точке (центр вневписанной окружности).

Если F - точка пересечения внешних углов ABC, то AF - биссектриса внутреннего угла A.

I - точка пересечения внутренних биссектрис (инцентр).

Внутренние биссектрисы пересекаются под углом BIC =90 +A/2

(A+B+C=180 => A/2 +B/2 +C/2 =90 => BIC =180 -B/2 -C/2 =90 +A/2)

Биссектрисы внутреннего и внешнего углов перпендикулярны.

BICF - вписанный (противоположные углы прямые) =>

BIC+CFB=180 => CFB =90 -A/2

Тогда CAF =A/2 =90-CFB =90-60 =30°