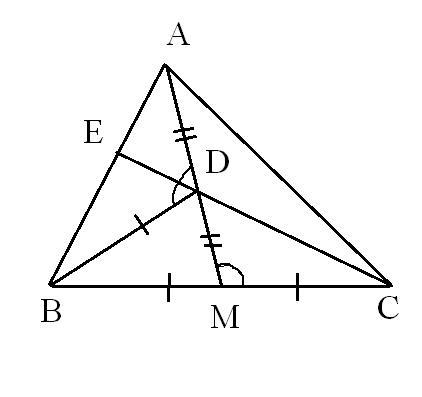
9.Пусть AM — медиана треугольника ABC, D— середина отрезка AM, E— точка пересечения прямой CD со стороной AB. Оказалось, что BD = BM . Докажите, что ∠BAD = ∠MDC

Ответ:

Пошаговое объяснение:

D— середина отрезка AM⇒AD=DM

AM — медиана⇒BM=MC

BD = BM=MC⇒BD=MC

BD = BM⇒ΔBMD-равнобедренный⇒∠BMD=∠BDM

∠CMD=180°-∠BMD=180°-∠BDM=∠BDA⇒∠BDA=∠CMD

∠BDA=∠CMD; BD=MC; AD=DM⇒ΔBDA=ΔCMD(по 1-му признаку равенства треугольников)

ΔBDA=ΔCMD⇒∠BAD = ∠MDC

ч.т.д

К чему точка Е, не понятно