Предмет: Математика, автор: usmanova20205

12.решите систему уравнения

Приложения:

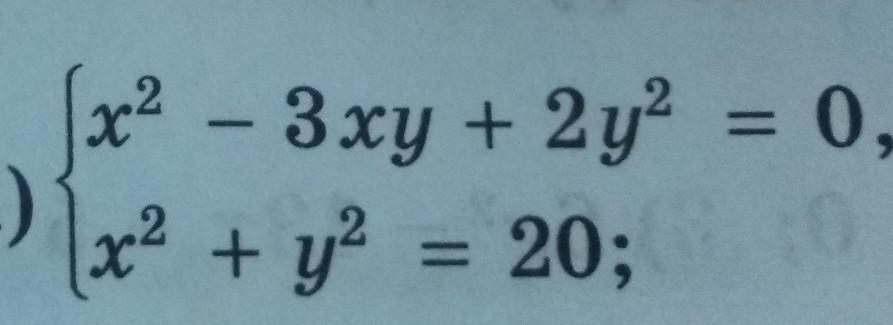
Ответы

Автор ответа: DNHelper

Ответ:

(√10, √10), (-√10, -√10), (4, 2), (-4, -2)

Пошаговое объяснение:

Рассмотрим первое уравнение, его левую часть:

$x^2-3xy+2y^2=x^2-2xy-xy+2y^2=x(x-2y)-y(x-2y)=\\=(x-y)(x-2y)$

Тогда система имеет вид:

$\displaystyle \left \{ {{(x-y)(x-2y)=0,} \atop {x^2+y^2=20}} \right.$

$\displaystyle \left \{ {{x=y,} \atop {x^2+y^2=20}} \right.\\\left \{ {{x=y,} \atop {x^2+x^2=20}} \right. \\\left \{ {{x=y,} \atop {2x^2=20}} \right. \\\left \{ {{x=y} \atop {x^2=10}} \right.\\\left \{ {{y=\pm\sqrt{10}} \atop {x=\pm\sqrt{10}}} \right.$ ИЛИ $\displaystyle \left \{ {{x=2y,} \atop {x^2+y^2=20}} \right.\\\left \{ {{x=2y,} \atop {4y^2+y^2=20}} \right. \\\left \{ {{x=2y,} \atop {5y^2=20}} \right. \\\left \{ {{x=2y,} \atop {y^2=4}} \right. \\\left \{ {{x=\pm4} \atop {y=\pm2}} \right.$