Предмет: Алгебра,
автор: lovkach343
Решить с пояснениями.80 Баллов
Приложения:
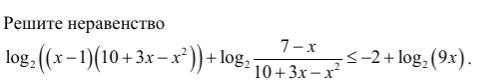
Ответы
Автор ответа:
1
Ответ:
Объяснение:
ODZ:
основание 2>1, y=log₂x возраст, знак не меняем
D=b^2-4ac=529-4*4*28=529-448=81
учитывая ОДЗ, получаем ответ:
Интересные вопросы
Предмет: Русский язык,
автор: alkantaro
Предмет: Английский язык,
автор: Поля4488
Предмет: Русский язык,
автор: ольга349
Предмет: Литература,
автор: Лев11167
Предмет: Русский язык,
автор: лера2437