Предмет: Математика, автор: Аноним

Докажите:
Докажите:
Докажите:
Ребят, желательно по подробнее, я хочу понять
Пожалуйста (

Приложения:

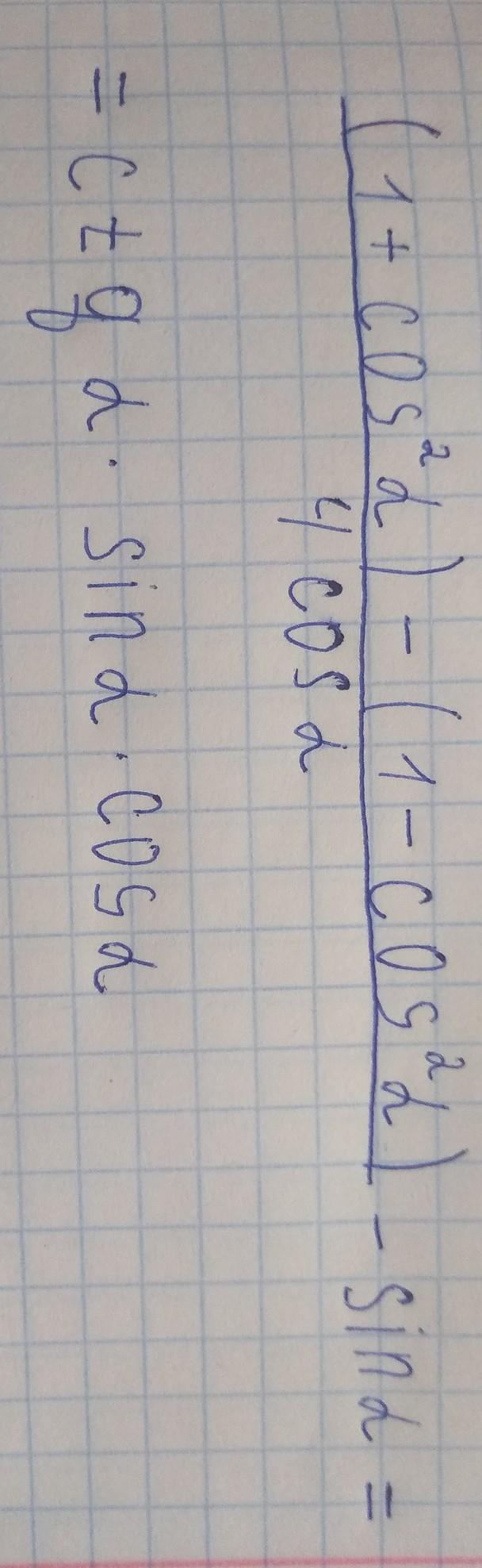
LFP: а у вас выражение ВЕРНО переписано...?? справа получается косинус в квадрате... а слева ничего похожего)) лучше фото задания...

Ответы

Автор ответа: NNNLLL54

3

Ответ:

$\star \ \displaystyle \frac{(1+cos^2a)-(1-cos^2a)}{4\, cosa}-sina=\frac{2cos^2a}{4\, cosa}-sina=\frac{cosa}{2}-sina=\\\\\\=\frac{cosa-2sina}{2}\ ;\\\\\\\star \ ctga\cdot sina\cdot cosa=\frac{cosa}{sina}\cdot sina\cdot cosa=cos^2a=\frac{1+cos2a}{2}\ ;\\\\\\\star \ \ \frac{cosa-2sina}{2}\ne \frac{1+cos2a}{2}$

$\displaystyle \star \ \ \frac{(1+cos^2a)-(1-cos^2a)}{4\, cosa}-sina=\frac{1+(cos^2a-sin^2a)}{4\, cosa}-sina=\\\\\\=\frac{1+cos2a}{4\, cosa}-sina=\frac{1+cos2a-4sina\, cosa}{4\, cosa}\ \ne \frac{1+cos2a}{2}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Биология, автор: Shiroika

1. Какое растение распространяет плоды и семена по воде?
Стрелолист
Клён
Фиалка
Недотрога

2. Какое растение распространяет семена по воздуху?
Фиалка
Клён
Недотрога
Стрелолист

3. Какое растение распространяет плоды и семена с помощью животных?
Клён
Стрелолист
Недотрога
Фиалка

СРОЧНО

2 года назад

Предмет: Физика, автор: anime4

как пишется этот знак @ помогите пж

2 года назад

Предмет: Английский язык, автор: Vanil119

помогите перевести пожалуйста?????

2 года назад

Предмет: Алгебра, автор: sharik10

Помогите, пожалуйста. Даю 10 баллов :)

8 лет назад

Предмет: Математика, автор: RA1004

Найдите площадь параллелограмма АВСD если АВ=6,5 АС=8 а угол А 45 градусам

8 лет назад