помогите пожалуйста решить!
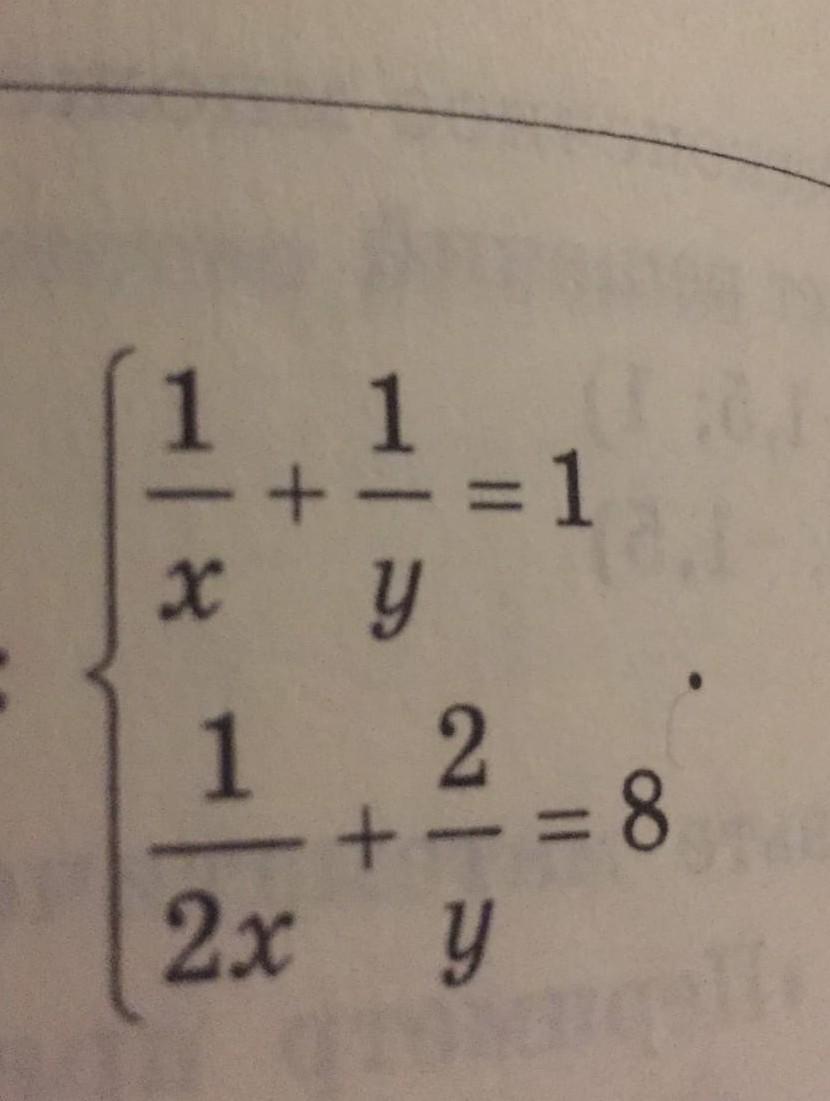
Ответы
ЗАДАНИЕ:
Решить систему уравнений:
1/x + 1/y = 1 && 1/(2x) + 2/y = 8
РЕШЕНИЕ:
Выразим y через x из первого уравнения:
1/y = 1 - 1/x
Умножаем обе части уравнения на y с добавлением условия y != 0:
1 = y * (1 - 1/x) && y != 0
y = 1 / (1 - 1/x) && y != 0
Подставляем полученное выражение для y во второе уравнение:
1/(2x) + 2 / [1 / (1 - 1/x)] = 8
Умножаем обе части уравнения на x с добавлением условия 2x != 0:
1 + 4x / [1 / (1 - 1/x)] = 16x && 2x != 0
1 + 4x * (1 - 1/x) = 16x && x != 0
1 + 4x - 4 = 16x && x != 0
-3 = 12x && x != 0
x = - 1/4
Подставляем полученное значение x в выражение для y:
y = 1 / (1 - 1/[-1/4]) && y != 0
y = 1 / (1+4) && y != 0
y = 1/5
ОТВЕТ:
x = - 1/4 && y = 1/5
При желании, дополнительно можно сделать проверку, подставив полученные значения в исходные уравнения системы, и удостовериться что достигается равенство левых и правых частей.