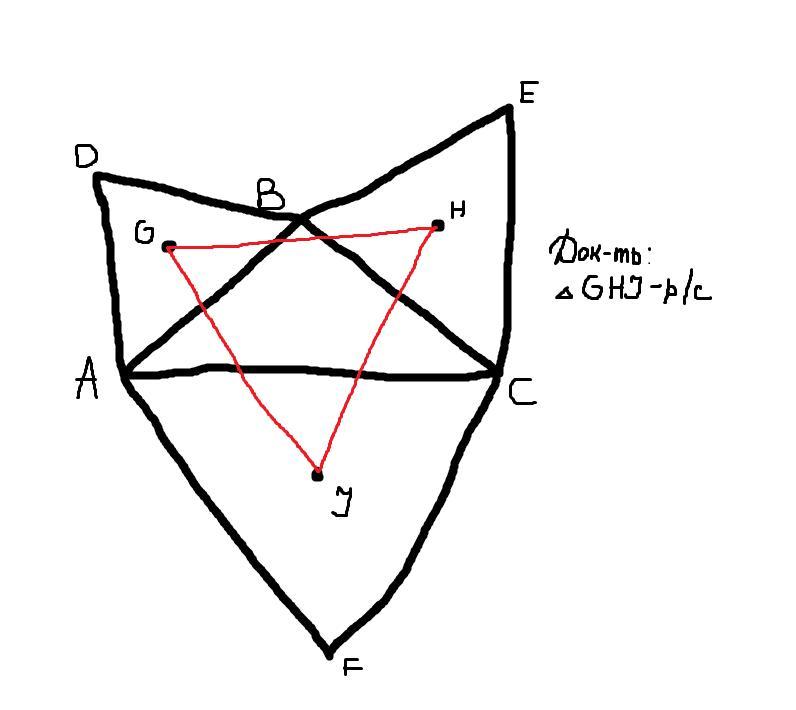
Доказать, что треугольник GHJ равносторонний.

На сторонах треугольника ABC вовне построены равносторонние треугольники. Доказать, что их центры образуют равносторонний треугольник (теорема Наполеона).

Окружности ADB и BEC вторично пересекаются в точке T.

ADBT, BECT - вписанные четырехугольники.

Сумма углов вписанного четырехугольника 180.

∠ATB =∠BTC =180-60 =120

Тогда ∠ATC =360-120-120 =120

=> AFCT - вписанный четырехугольник (т.к. ∠ATC+∠F=180)

Точка T лежит на окружности AFC.

Линия центров двух окружностей перпендикулярна общей хорде.

GJ⊥AT, GH⊥BT, HJ⊥CT

∠ATB=∠BTC=∠ATC=120 => ∠G=∠H=∠J=60 => △GHJ - равносторонний.