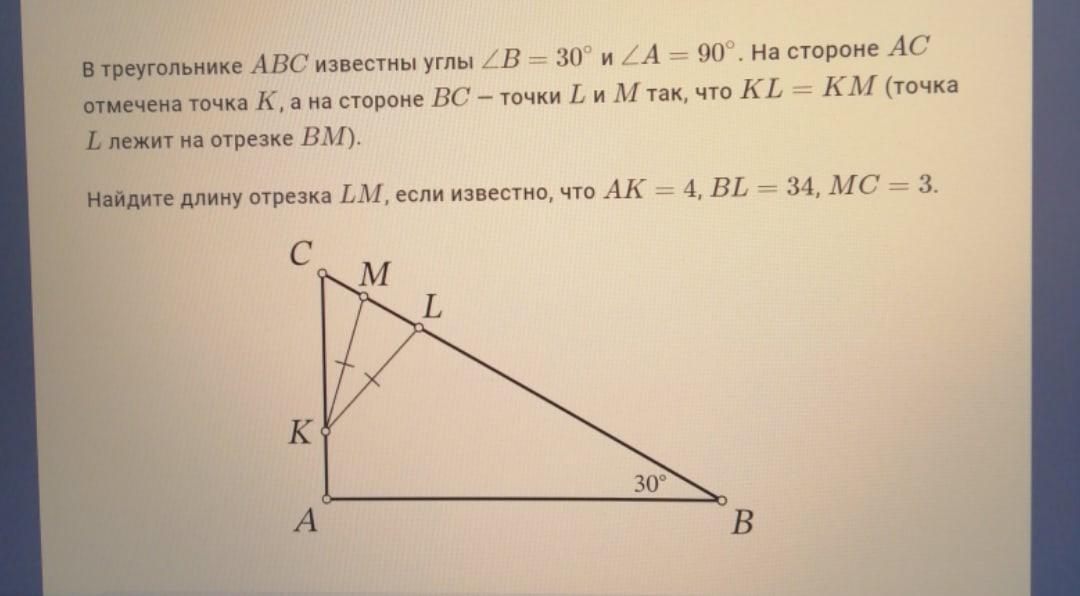
В треугольнике ABC известны углы ∠B=30∘ и ∠A=90∘. На стороне AC отмечена точка K, а на стороне BC — точки L и M так, что KL=KM (точка L лежит на отрезке BM).

Найдите длину отрезка LM, если известно, что AK=4, BL=34, MC=3.

Ответ:

Ответ: 15 см.

Пошаговое объяснение:

В прямоугольном треугольнике АВС второй острый угол САВ равен:

∠ САВ = 90° - ∠ В = 90° - 30° = 60°.

В прямоугольном треугольнике ACD второй острый угол CAD равен:

∠ CAD = 90° - ∠ CDA = 90° - 60° = 30°.

Катет CD = 5 см и лежит напротив этого угла. Из этого следует, что гипотенуза AD = 2 * 5 = 10 (см).

Рассмотрим треугольник ADB, в нём:

∠ В = 30°,

∠ DAB = ∠ CAB - ∠ CAD = 60° - 30° = 30°.

Получаем, что треугольник ADB – равнобедренный, AD = BD = 10 (см).

BC = CD + BD = 5 + 10 = 15 (см).

Ответ: катет ВС равен 15 см.