Найти частное решение (частных интеграл) дифференциального уравнения
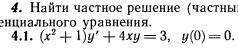
Ответы
Ответ: y=(x³+3*x)/(x²+1)².
Пошаговое объяснение:
Перепишем уравнение в виде: y'+4*x*y/(x²+1)-3/(x²+1)=0. Это - ЛДУ 1 порядка, полагаем y=u*v. Тогда y'=u'*v+u*v' и уравнение принимает вид: u'*v+u*v'+4*x*u*v/(x²+1)-3/(x²+1)=0, или v*[u'+4*x*u/(x²+1)]+u*v'-3/(x²+1)=0. Так как одной из функций u или v мы можем распорядиться произвольно, то поступим так с u и потребуем, чтобы она удовлетворяла уравнению u'+4*x*u/(x²+1)=0, или du/u=-4*x*dx/(x²+1)=-2*d(x²+1)/(x²+1). Интегрируя, находим u=1/(x²+1)². Подставляя теперь это выражение в уравнение u*v'=3/(x²+1), получаем уравнение v'=3*(x²+1), или dv=3*x²*dx+3*dx. Интегрируя, находим v=x³+3*x+C, где C - произвольная постоянная. Отсюда y=u*v=(x³+3*x+C)/(x²+1)². Используя теперь условие y(0)=0, приходим к уравнению C/1=0, откуда C=0. Тогда искомое частное решение y=(x³+3*x)/(x²+1)².