Помогите пж пределы выш мат
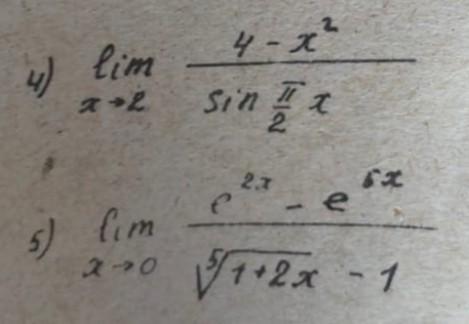
Ответы
Ответ: 4) 8/π; 5) -10.
Пошаговое объяснение:
4) Подстановка x=0 в данное выражение приводит к неопределённости вида 0/0. Для её раскрытия прежде всего заметим, что 4-x²=(2+x)*(2-x). Так как предел выражения 2+x при x⇒2 равен 4, то данный предел равен 4*lim(x⇒2)[(2-x)/sin(π*x/2)]. Положим 2-x=z, тогда при x⇒2 z⇒0 и данный предел равен 4*lim(z⇒0)[z/sin(π-π*z/2)]=4*lim(z⇒0)[z/sin(π*z/2)]. Положим, наконец, π*z/2=t, тогда z=2*t/π и при z⇒0 t⇒0. Тогда данный предел равен 4*2/π*lim(t⇒0)[t/sin(t)]=8/{π*lim(t⇒0)[sin(t)/t]}. Но последний предел есть ни что иное, как первый замечательный предел, который равен 1. Отсюда искомый предел равен 8/π.
5) Подстановка x=0 в данное выражение приводит к неопределённости вида 0/0. Для её раскрытия прежде всего заметим, что e^(2*x)-e^(6*x)=e^(2*x)*[1-e^(4*x)]=e^(2*x)*[1+e^(2*x)]*[1-e^(2*x)]=e^(2*x)*[1+e^(2*x)]*(1+e^x)*(1-e^x). Так как предел произведения e^(2*x)*[1+e^(2*x)]*(1+e^x) при x ⇒0 равен 1*2*2=4, то данный предел равен 4*lim(x⇒0) [1-e^x)/[(1+2*x)^(1/5)-1]. А так как a⁵-b⁵=(a-b)*(a⁴+a³*b+a²*b²+a*b³+b⁴), то, полагая (1+2*x)^(1/5)=a и 1=1^(1/5), умножим числитель и знаменатель на выражение (1+2*x)^(4/5)+(1+2*x)^(3/5)+(1+2*x)^(2/5)+(1+2*x)^(1/5)+1. После этого данное выражение можно записать в виде: 4*lim(x⇒0){(1-e^x)*[(1+2*x)^(4/5)+(1+2*x)^(3/5)+(1+2*x)^(2/5)+(1+2*x)^(1/5)+1]}/(2*x). Так как при x⇒0 1+2*x⇒1, то данный предел равен 20*lim(x⇒0)[(1-e^x)/(2*x)]=10*lim(x⇒0)[(1-e^x)/x]. Пусть 1-e^x=-t, тогда e^x=t+1, x=ln(t+1) и при x⇒0 t⇒0. Тогда данный предел равен 10*lim(t⇒0)[-t/ln(1+t)]=-10*lim(t⇒0)[t/ln(t+1)]=-10/lim(t⇒0)[ln(t+1)/t]. Обозначим A=lim(t⇒0)[ln(t+1)/t]. Рассмотрим B=e^A=lim(t⇒0)[(t+1)^(1/t)]. Это есть ни что иное, как второй замечательный предел, то есть B=e. Из равенства e^A=e находим A=1, откуда искомый предел равен -10/1=-10.