Предмет: Алгебра, автор: Djdjdhfh

найти площадь фигуры ограниченных линиями

Приложения:

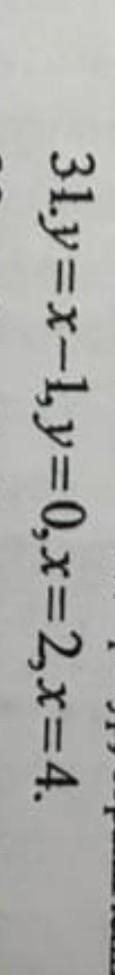
Ответы

Автор ответа: NNNLLL54

Ответ:

$y=x-1\ \ ,\ \ y=0\ \ ,\ \ x=2\ \ ,\ \ x=4$

$\displaystyle S=\int\limits^4_2\, (x-1)\, dx=\Big(\frac{x^2}{2}-x\Big)\Big|_2^4=\frac{16}{2}-4-\frac{4}{2}+2=8-4-2+2=4$

P.S. Можно проверить, вычислив площадь полученной области, как площадь трапеции:

$S=\dfrac{a+b}{2}\cdot h=\dfrac{2+4}{2}\cdot (4-2)=\dfrac{6}{3}\cdot 2=2\cdot 2=4$ .

Приложения:

Интересные вопросы

Предмет: Русский язык, автор: gumagalieva50

2 года назад

Предмет: Қазақ тiлi, автор: Аноним

2 года назад

Предмет: Окружающий мир, автор: машанезнайка

2 года назад

Предмет: Английский язык, автор: 77melnic77

8 лет назад

Предмет: Экономика, автор: yuliabykova1982

8 лет назад