Предмет: Математика, автор: VSEVIKUS

Вычислить первым замечательным пределом
Вторая попытка на хороший ответ

Приложения:

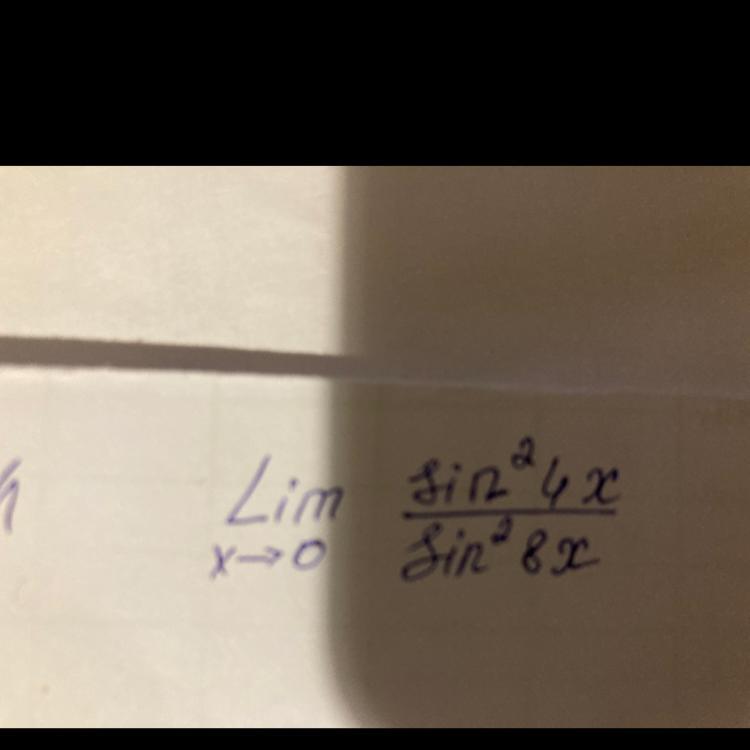
Ответы

Автор ответа: Matematiktm

Ответ:

Пошаговое объяснение:

$lim_{x \to 0} \frac{sin^{2} 4x}{sin^{2} 8x}=lim_{x \to 0} \frac{sin 4x}{sin 8x}*lim_{x \to 0}\frac{sin 4x}{sin 8x}=lim_{x \to 0} \frac{\frac{sin 4x}{4x} *4x}{\frac{sin 8x}{8x} *8x}*lim_{x \to 0} \frac{\frac{sin 4x}{4x} *4x}{\frac{sin 8x}{8x} *8x}=\frac{lim_{x \to 0} \frac{sin 4x}{4x} }{lim_{x \to 0} \frac{sin 8x}{8x} *2}*\frac{lim_{x \to 0} \frac{sin 4x}{4x} }{lim_{x \to 0} \frac{sin 8x}{8x} *2}=\frac{1}{4}$

$\frac{lim_{x \to 0} \frac{sin 4x}{4x} }{lim_{x \to 0} \frac{sin 8x}{8x} }=\frac{lim_{u \to 0} \frac{sin u}{u} }{lim_{v \to 0} \frac{sin v}{v} }=1$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: 79787340160

нужно название реки в Крыму начинается с буквы =С= четвертая буква=Ы= шестая буква=З=а последняя буква=Ь= СПАСИБО!

2 года назад

Предмет: Русский язык, автор: ary03

составить свой текст Правила дорожного движения

2 года назад

Предмет: Русский язык, автор: lilpetrosyan0

Выделите приставки в следующих словах.
Въезд. выехал. переезжать. съесть. объявление. заявление. сверхъестественный. съёмка. уезжать.

Вычислить первым замечательным пределом Вторая попытка на хороший ответ

Ответы

Вычислить первым замечательным пределом
Вторая попытка на хороший ответ