Предмет: Геометрия,
автор: гггггг
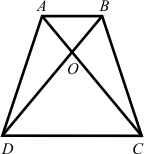
На рисунке 165 АВ || CD. а) Докажите, что АО : ОС = ВО : OD. б) Найдите АВ, если OD = 15 см, ОВ = 9 см, CD = 25 см.
Прошу решите на листочке с дано с решением и сфоткайте, просто когда тут написано мне не удобно
срочно помигете умоляю
Приложения:
Ответы
Автор ответа:
0
∠АВО = ∠CDO как накрест лежащие при пересечении АВ║CD секущей BD,
∠АОВ = ∠COD как вертикальные, ⇒
ΔАОВ подобен ΔCOD по двум углам.
Отношения соответствующих сторон равны:
АО : СО = ОВ : OD = АВ : CD
ОВ : OD = АВ : CD
9 : 15 = АВ : 25
АВ = 9 · 25 / 15 = 15 см
∠АОВ = ∠COD как вертикальные, ⇒
ΔАОВ подобен ΔCOD по двум углам.
Отношения соответствующих сторон равны:
АО : СО = ОВ : OD = АВ : CD
ОВ : OD = АВ : CD
9 : 15 = АВ : 25
АВ = 9 · 25 / 15 = 15 см
Интересные вопросы
Предмет: Алгебра,
автор: tumkag20
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: polinasuhorukova0
Предмет: Математика,
автор: cfif3000
Предмет: Биология,
автор: Света24311