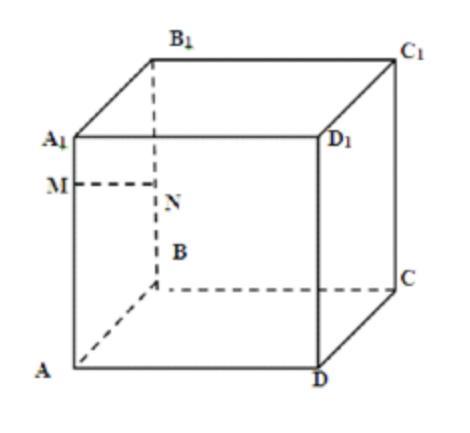
Дан куб ABCDA1B1C1D1. Сколько плоскостей, определяемых всеми гранями куба, пересекает прямая MN, если MN не параллельна A1B1?

а) 2
б) 3
в) 4
г) 5

Ответ:

в) 4

Объяснение:

Есть три возможных взаимных расположения прямой и плоскости:

• прямая параллельна плоскости, т.е. прямая не имеет общих точек с плоскостью;
• прямая пересекает плоскость, т.е. одна общая точка;
• прямая лежит в плоскости.

Точка М лежит в грани AA₁D₁D, значит прямая MN пересекает эту грань.

Точка N лежит в грани ВВ₁С₁С, значит прямая MN пересекает эту грань.

Прямая MN не параллельна прямой А₁В₁, значит она пересекает грани A₁B₁C₁D₁ и ABCD.

Всего 4 грани.