Предмет: Алгебра, автор: cmx2s5vpzf

50 БАЛЛОВ СРОЧНО!!!!

Приложения:

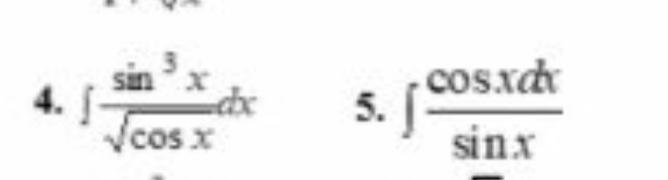
Ответы

Автор ответа: NNNLLL54

0

Ответ:

$\displaystyle 4)\ \ \int \frac{sin^3x}{\sqrt{cosx}}\, dx=\int sin^2x\cdot sinx\cdot (cosx)^{-\frac{1}{2}}\, dx=\\\\\\=\int (\underbrace{1-cos^2x}_{sin^2x})\cdot (cosx)^{-\frac{1}{2}}\cdot \underbrace{sinx\, dx}_{-d(cosx)}=-\int (\, (cosx)^{-\frac{1}{2}}-(cosx)^{\frac{3}{2}}\, )\cdot d(cosx)=\\\\\\=-2(cosx)^{\frac{1}{2}}+\frac{2(cosx)^{\frac{5}{2}}}{5}+C=-2\sqrt{cosx}+\frac{2\sqrt{cos^5x}}{5}+C$

$\displaystyle 5)\ \ \int \frac{cosx\, dx}{sinx}=\int \frac{d(sinx)}{sinx}=ln|sinx|+C\\\\\\\star \ \ \frac{cosx}{sinx}=ctgx\ \ \ \Rightarrow \ \ \ \int ctgx=ln|sinx|+C\ \ \star$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Окружающий мир, автор: utyyflbr

Что относится к сезонным явлениям природы?
1) восход Солнца
2) миграция птиц
3) приливы и отливы
4)извержение вулканов

2 года назад

Предмет: Другие предметы, автор: myshafilip

після уроку фізкультури два старшокласники попросили хлопчика постояти на дверях роздягальні щоб їм не заважали малявки після уроків учні 7-б розказували що на уроці фізкультури у декого з них зникли гроші
яких помилок допустився хлопчик що ви порадите йому робити

2 года назад

Предмет: Русский язык, автор: nikitosikteremok

На месте каких согласных звуков при записи слов буквами будут опасными. Покажи эти опасные места- мука, лук, миска, шутка, лапка, свечка.

2 года назад

Предмет: Химия, автор: Книголюбитель

Умоллляяю(((
Сравните угловые связи, строение молекул H2S и SO2 и объясните причину этих различий

8 лет назад

Предмет: Геометрия, автор: ДАпруган

Даны две перпендикулярные плоскости.Найдите расстояние от точки А до линии пересечения этих плоскостей,если точка А находиться на расстояниях корень из 5 и 2 см от этих плоскостей )Можно с рисунком пожалуйста!!!!!

8 лет назад