Предмет: Геометрия,
автор: pilel
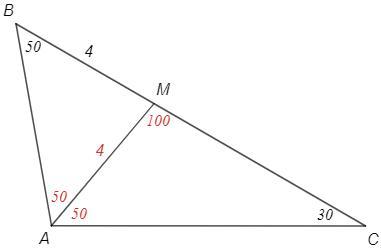
В треугольнике ABC проведена биссектриса AM. ∠ACB = 30°, ∠CBA = 50°, BM = 4 см. Выполните рисунок и найдите:
а) длину биссектрисы AM (10 баллов);
б) длину стороны AС (12 баллов);
в) радиус окружности, описанной около треугольника ABC (11 баллов).
Ответы
Автор ответа:
46
a)
∠BAC =180-B-C =180-50-30 =100
∠BAM =∠BAC/2 =50 (AM - биссектриса ∠BAC)
∠BAM=∠B => △BMA - равнобедренный, AM=BM=4 (см)
б)
∠AMC =50+50 =100 (внешний угол △BMA)
△AMD, теорема синусов
AM/sinC =AC/sinAMC => AC =4 sin100/sin30
=8 sin100° =8 cos10° ~7,8785 (см)
в)
△ABC, теорема синусов
AC/sinB =2R => R =8 sin100/2 sin50
=4 sin(2*50)/sin50
=4 2sin50cos50/sin50
=8 cos50° ~5,1423 (см)
Приложения:
juliabarhatova787:
https://znanija.com/task/46651056
А радиус чему равен будет в итоге? 3 или 5,14??
R= 8 cos50° ~ 5,1423
угол не табличный, в ответе следует оставить cos50
приближенное значение я даю для проверки
R =AB >4, это должно быть понятно
Да, я так и сдала
Помотрим, что поставят
Спасибо, у меня пятерка) Я в ответ написала примерно 5,14= радиус
кто может скинуть ответы на все 4 задания из геометрии на 15 неделю? вк: taisia1007. кому проверили
Интересные вопросы
Предмет: Қазақ тiлi,
автор: derevyagina11
Предмет: Другие предметы,
автор: алина1963
Предмет: Русский язык,
автор: калабоксказка
Предмет: Геометрия,
автор: petritsya97