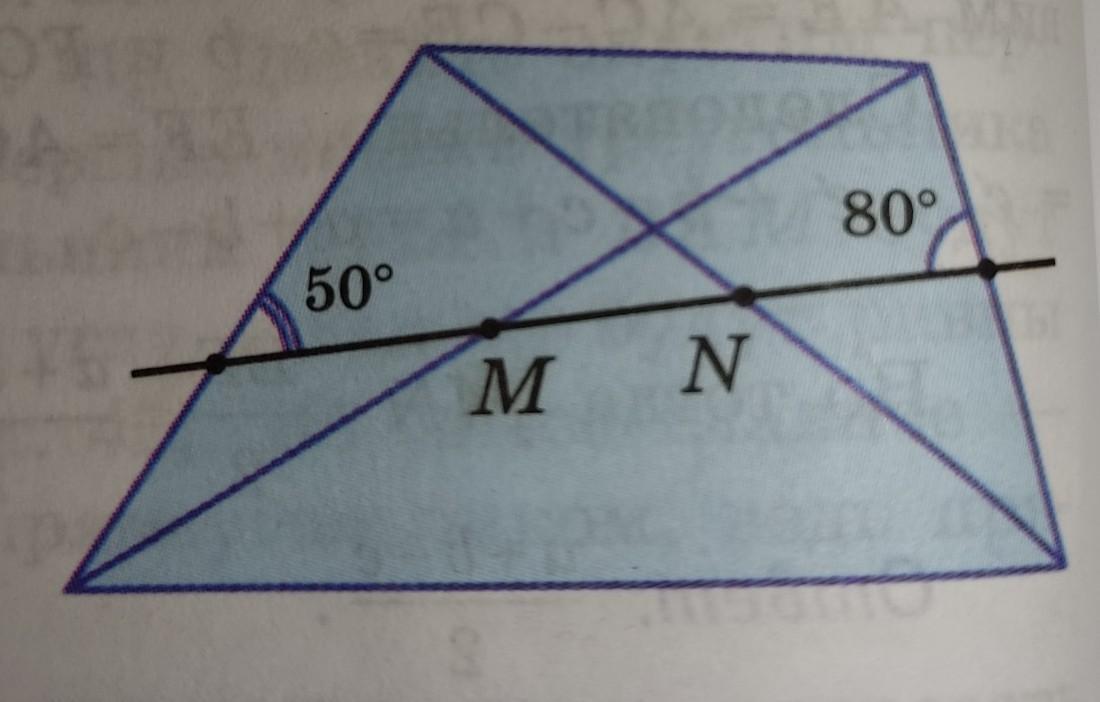
*Прямая, проходящая через середины М и N диагоналей четырёх- угольника, образует с его сторонами углы 50° и 80°. Докажите, что отре- Зок MN равен половине одной из сто- рон четырёхугольника. (» рис.)​

Объяснение:

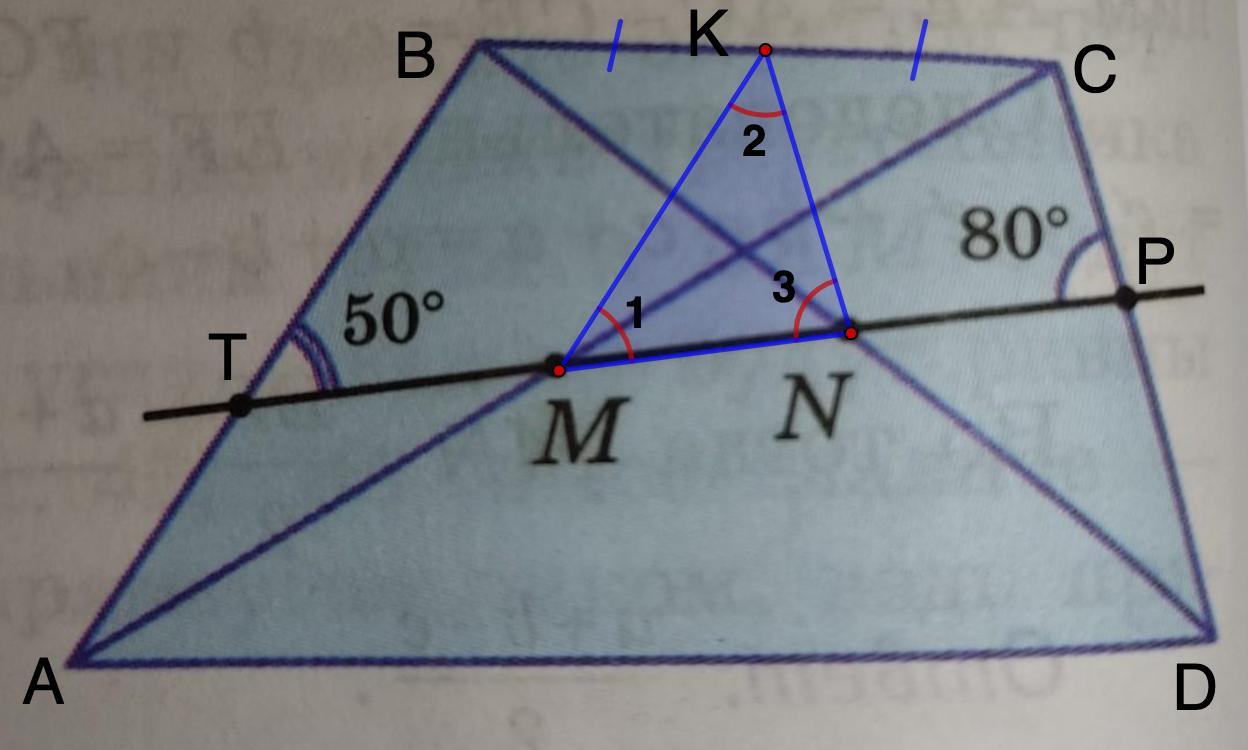
Дано: ABCD - четырехугольник.

АМ = МВ; DN = ND;

∠ВТМ = 50°; ∠СРN = 80°;

Доказать:

Доказательство:

Отметим точку К - середину ВС. Соединим К с точками М и N.

1. Рассмотрим ΔDBC.

BK = KC (построение)

BN = ND (условие)

⇒ NK - средняя линия ΔDBC.

Средняя линия треугольника параллельна основанию и равна его половине.

⇒ NK || CD

2. Аналогично, МК - средняя линия ΔАBC.

⇒ МК || АВ.

3. Рассмотрим ΔMKN.

∠1 = ∠ВТМ = 50° (соответственные при АВ || MK и секущей TP)

∠3 = ∠CPN = 80°  (соответственные при KN || CD и секущей TP)

• Сумма углов треугольника равна 180°.

⇒ ∠2 = 50°

• Если у треугольника два угла равны, то этот треугольник — равнобедренный.

⇒ ΔMKN - равнобедренный.