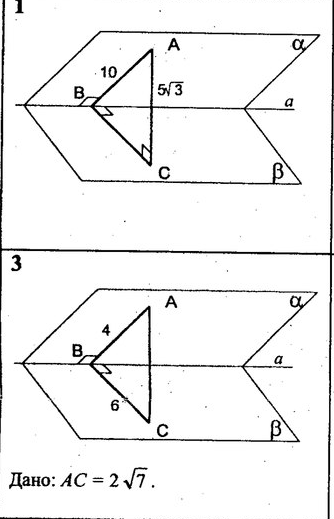
Плоскости альфа и бетта пересекаются по прямой альфа.Найти угол между плоскостями альфа и бетта.

Определение: Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
В нашем случае плоскость АВС перпендикулярна обеим плоскостям (так как АВ и СВ перпендикулярны линии пересечения плоскостей) Искомый угол - это угол АВС = α.
1. В прямоугольном треугольнике АВС Sinα=AC/AB.
Sinα=5√3/10=√3/2.
Ответ: α=arcsin(√3/2) = 60°.
2. В треугольнике АВС по теореме косинусов:
Cosα=(a²+b²-c²)/(2*a*b) или
Cosα=(36+16-28)/(2*4*8)=1/2.
Ответ: α=arccjs(1/2) = 60°.