Предмет: Алгебра, автор: timofeevakatya166

.............Решите...

Приложения:

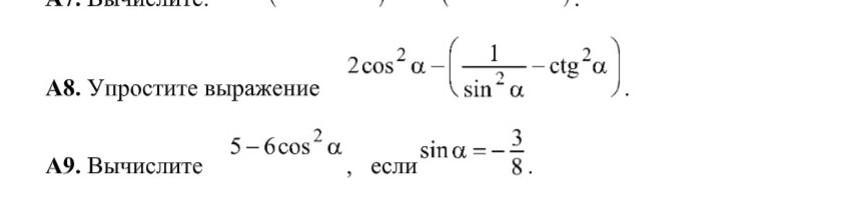
Ответы

Автор ответа: Universalka

0

$\displaystyle\bf\\8) \ 2Cos^{2} \alpha -\Big(\frac{1}{Sin^{2} \alpha } -Ctg^{2} \alpha \Big)=2Cos^{2} \alpha -\Big(1+Ctg^{2} \alpha -Ctg^{2} \alpha \Big)=\\\\2Cos^{2}\alpha -1 =2Cos^{2} \alpha-(Sin^{2} \alpha +Cos^{2} \alpha)=2Cos^{2}\alpha -Sin^{2} \alpha -Cos^{2} \alpha =\\\\\\=Cos^{2} \alpha -Sin^{2} \alpha =Cos2\alpha \\\\\\9) \ 5-6Cos^{2} \alpha =5-6\cdot(1-Sin^{2} \alpha )=5-6+6Sin^{2}\alpha =\\\\=6Sin^{2} \alpha -1=6\cdot\Big(-\frac{3}{8} \Big)^{2} -1=6\cdot\frac{9}{64} -1=$

$\displaystyle\bf\\=\frac{54}{64} -1=0,84375-1=-0,15625$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: Ангелочик11

Из каждого предложения выпишите словосочетание

один муравей даже залез мне на колено и грелся на солнышке. Перед самым моим носом воздухе беззаботно летал мошкара.По скамейке бегал черненький муравей.Над клумбой порхала бабочка.

2 года назад

Предмет: Русский язык, автор: незнайка1820

как проверить букву о в слове собираются

2 года назад

Предмет: Английский язык, автор: ник11371

посмотри на часы.назови время.скажи,что тыобычно делаешьв это время.как ты думаешь ,что Джим и Джилл делают в это время

2 года назад

Предмет: Математика, автор: 66ygggghhjj

составьте по схеме выражения и найдите его значение

8 лет назад

Предмет: Алгебра, автор: annafyodorova

Очень срочно. Даю дофига баллов.
Помогите решить методом группировки

8 лет назад