Предмет: Алгебра, автор: villiwonkka1

145
_._._._._._._._._._

Приложения:

Ответы

Автор ответа: natalyabryukhova

2

Объяснение:

$1) y=(x^2+1)^5\\\\y'=5(x^2+1)^4*(x^2+1)'=5(x^2+1)^4*2x=10x(x^2+1)^4$

$\displaystyle 2)y=ln\;cosx\\\\y'=\frac{(cosx)'}{cosx}= \frac{-sinx}{cosx} =-tgx$

$\displaystyle 3) y=\sqrt{5x-7} =(5x-7)^{\frac{1}{2} }\\\\y'=\frac{1}{2}(5x-7)^{-\frac{1}{2} } *(5x-7)'=\frac{1}{2(5x-7)^{\frac{1}{2} }} *5=\frac{5}{2\sqrt{5x-7} }$

$\displaystyle 4)y=\sqrt{tg(2x-3)}=(tg(2x-3))^{\frac{1}{2} } \\\\y'=\frac{1}{2}(tg(2x-3))^{-\frac{1}{2} } *(tg(2x-3))'=\\\\=\frac{1}{2(tg(2x-3))^{\frac{1}{2} }} *\frac{(2x-3)^'}{cos^2(2x-3)} =\\\\=\frac{1}{2\sqrt{tg(2x-3)} } *\frac{2}{cos^2(2x-3)}=\frac{1}{\sqrt{tg(2x-3)}*cos^2(2x-3) }$

Использованы формулы:

$\displaystyle (x)^n=nx^{n-1}\\\\(cosx)'=-sinx\\\\(cx)'=c,\;\;\;c=const\\\\(c)'=0\\\\$

Приложения:

Предыдущий вопрос

Следующий вопрос

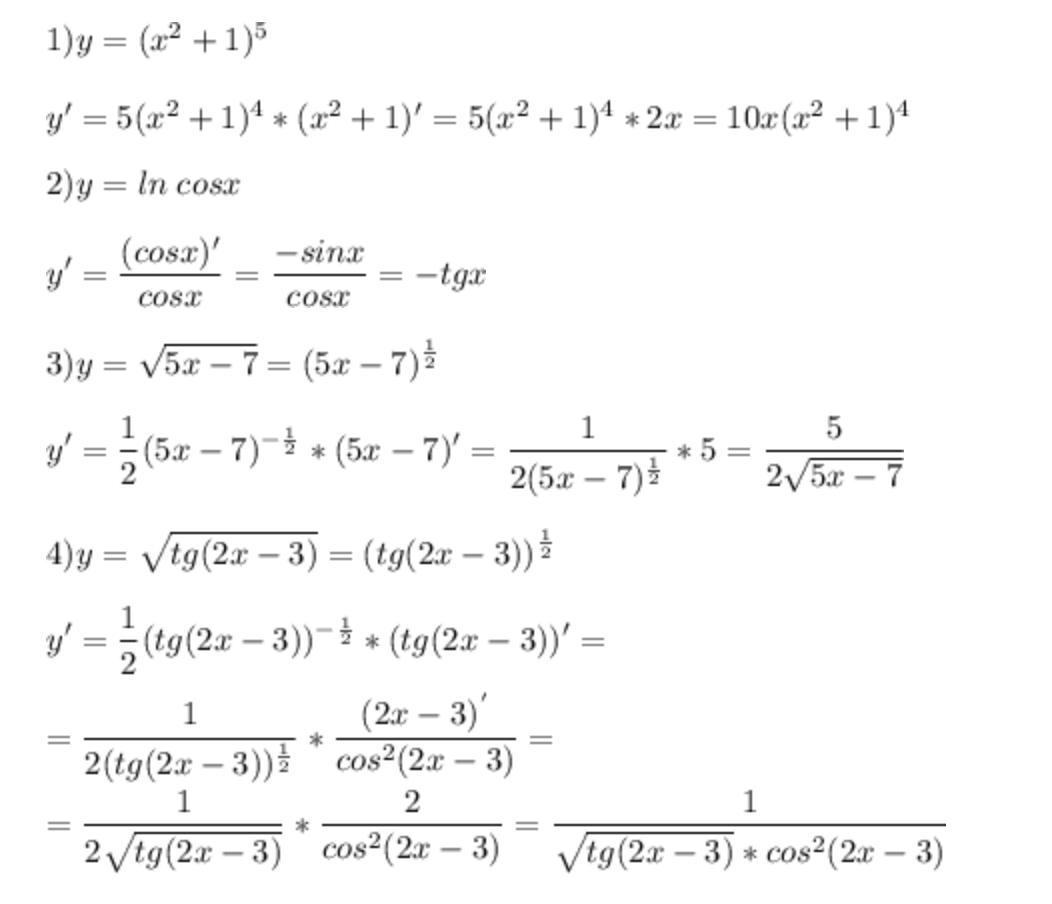
Интересные вопросы

Предмет: Русский язык, автор: Эльяночка124

помогите пожалуйста !!!!!
напишите сочинения на тему <<Одуванчик>>

2 года назад

Предмет: Другие предметы, автор: НикитаБарса

Составьте небольшую песню с именем ДАША!Заранее спасибо)))

2 года назад

Предмет: Українська мова, автор: angelina1122

Яка роль відокремлених членів у реченні?

2 года назад

Предмет: Русский язык, автор: viktoriadifiorpestdw

запишите текст,составленный по рисункам упражнения 21

8 лет назад

Предмет: Алгебра, автор: alajuann

решите срочно, пожалуйста. Даю 25 баллов

8 лет назад